题目内容
10.在△ABC内部随机取一点P,则事件“△PBC”的面积不大于△ABC面积的$\frac{1}{4}$”的概率是( )| A. | $\frac{7}{16}$ | B. | $\frac{9}{16}$ | C. | $\frac{5}{9}$ | D. | $\frac{4}{9}$ |
分析 先求出“△PBC的面积等于△ABC面积的$\frac{1}{4}$时,对应的位置,然后根据几何概型的概率公式求相应的面积,即可得到结论
解答 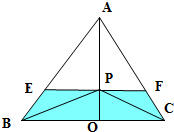 解:作出△ABC的高AO,当“△PBC的面积等于△ABC面积的$\frac{1}{4}$”时,此时OP=$\frac{1}{4}$OA,
解:作出△ABC的高AO,当“△PBC的面积等于△ABC面积的$\frac{1}{4}$”时,此时OP=$\frac{1}{4}$OA,
要使““△PBC的面积不大于△ABC面积的$\frac{1}{4}$”,则P位于阴影部分,
则△AEF的面积S1=($\frac{3}{4}$)2S=$\frac{9}{16}$S,
则阴影部分的面积为S-$\frac{9}{16}$S=$\frac{7}{16}$S,
则根据几何概型的概率公式可得“△PBC的面积小于不大于△ABC面积的$\frac{1}{4}$”的概率是:$\frac{\frac{7}{16}S}{S}=\frac{7}{16}$;
故选:A
点评 本题主要考查几何概型的概率公式的计算,根据面积之间的关系是解决本题的关键.

练习册系列答案
相关题目
18.已知中心在坐标原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1、F2,这两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形,若|PF1|=10,设椭圆与双曲线的离心率分别为e1,e2,则e1+e2的取值范围是( )
| A. | ($\frac{5}{4}$,+∞) | B. | ($\frac{4}{3}$,+∞) | C. | ($\frac{3}{2}$,+∞) | D. | ($\frac{5}{3}$,+∞) |
20.已知M=$\int_0^1{\frac{1}{x+1}dx,N=\int_0^{\frac{π}{2}}{cosxdx}}$,由图示程序框图输出的S为( )
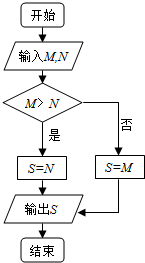

| A. | 1 | B. | ln2 | C. | $\frac{π}{2}$ | D. | 0 |
 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M、N分别是这段图象的最高点和最低点,且$\overrightarrow{OM}•\overrightarrow{ON}$=0(O为坐标原点),则A=$\frac{\sqrt{7}}{12}$π.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M、N分别是这段图象的最高点和最低点,且$\overrightarrow{OM}•\overrightarrow{ON}$=0(O为坐标原点),则A=$\frac{\sqrt{7}}{12}$π.