题目内容
18.已知不等式组$\left\{\begin{array}{l}x+y≥4\\ x-y≥-2\\ x≤2\end{array}\right.$表示的平面区域为D,点O(0,0),A(1,0).若点M是D上的动点,则$\frac{{\overrightarrow{OA}•\overrightarrow{OM}}}{{|{\overrightarrow{OM}}|}}$的最小值是( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{10}}}{10}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |
分析 利用向量的数量积将条件进行转化,利用数形结合进行求解即可得到结论.
解答 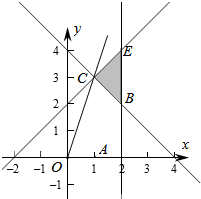 解:设z=$\frac{{\overrightarrow{OA}•\overrightarrow{OM}}}{{|{\overrightarrow{OM}}|}}$,则z=$\frac{{\overrightarrow{OA}•\overrightarrow{OM}}}{{|{\overrightarrow{OM}}|}}$=|$\overrightarrow{OA}$|•$\frac{\overrightarrow{OA}•\overrightarrow{OM}}{|\overrightarrow{OA}||\overrightarrow{OM}|}$=|$\overrightarrow{OA}$|•cos∠A0M,
解:设z=$\frac{{\overrightarrow{OA}•\overrightarrow{OM}}}{{|{\overrightarrow{OM}}|}}$,则z=$\frac{{\overrightarrow{OA}•\overrightarrow{OM}}}{{|{\overrightarrow{OM}}|}}$=|$\overrightarrow{OA}$|•$\frac{\overrightarrow{OA}•\overrightarrow{OM}}{|\overrightarrow{OA}||\overrightarrow{OM}|}$=|$\overrightarrow{OA}$|•cos∠A0M,
∵O(0,0),A(1,0).
∴|$\overrightarrow{OA}$|=1,
∴z=|$\overrightarrow{OA}$|•cos∠A0M=cos∠A0M,
作出不等式组对应的平面区域如图:
要使cos∠A0M,
则∠A0M最大,
即当M在C处时,∠A0M最大,
由$\left\{\begin{array}{l}{x+y=4}\\{x-y=-2}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$,即C(1,3),
则|AC|=$\sqrt{10}$,
则cos∠A0M=$\frac{1}{\sqrt{10}}$=$\frac{{\sqrt{10}}}{10}$,
故选:C.
点评 本题主要考查线性规划的应用,利用向量的数量积将条件进行转化是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.在花园小区内有一块三边长分别为6米、8米、10米的三角形绿化地,有一只小狗在其内部玩耍,若不考虑小狗的大小,则在任意指定的某时刻,小狗与三角形三个顶点的距离均超过2米的概率是( )
| A. | 1-$\frac{π}{24}$ | B. | 1$-\frac{π}{6}$ | C. | 1$-\frac{π}{12}$ | D. | 2$-\frac{π}{3}$ |
6.已知函数f(x)=cos(2x+φ)(φ为常数)为奇函数,那么cosφ=( )
| A. | -$\frac{{\sqrt{2}}}{2}$ | B. | 0 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 1 |
13.圆C:x2+y2+4x-2y+3=0的圆心坐标及半径分别是( )
| A. | (-2,1),$\sqrt{2}$ | B. | (2,1),$\sqrt{2}$ | C. | (-2,1),2 | D. | (2,-1),2 |
7.如图所示程序框图中,输出S=( )
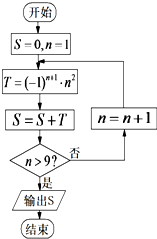

| A. | 45 | B. | 66 | C. | -66 | D. | -55 |
 如图,在直角坐标系中,曲线段AB是函数y=1-x2图象的一部分,P为曲线段AB上异于点A,B一个动点,PM丄x轴,垂足为M,PN丄y轴,垂足为N.
如图,在直角坐标系中,曲线段AB是函数y=1-x2图象的一部分,P为曲线段AB上异于点A,B一个动点,PM丄x轴,垂足为M,PN丄y轴,垂足为N.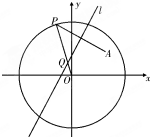 如图,已知点A为圆x2+y2=16内一定点,P是圆上任意一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是( )
如图,已知点A为圆x2+y2=16内一定点,P是圆上任意一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是( )