题目内容
7.如图所示程序框图中,输出S=( )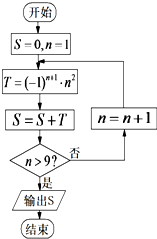
| A. | 45 | B. | 66 | C. | -66 | D. | -55 |
分析 根据程序框图的流程,可判断程序的功能是求S=12-22+32-42+…+(-1)n+1•n2,判断程序运行终止时的n值,计算可得答案.
解答 解:由程序框图知,第一次运行T=(-1)2•12=1,S=0+1=1,n=1+1=2;
第二次运行T=(-1)3•22=-4,S=1-4=-3,n=2+1=3;
第三次运行T=(-1)4•32=9,S=1-4+9=6,n=3+1=4;
…
直到n=9+1=10时,满足条件n>9,运行终止,此时T=(-1)10•92,
S=1-4+9-16+…+92-102=1+(2+3)+(4+5)+(6+7)+(8+9)-100=$\frac{1+9}{2}$×9-100=-55.
故选:D.
点评 本题考查了循环结构的程序框图,判断算法的功能是解答本题的关键,属于基础题.

练习册系列答案
相关题目
17.函数f(x)=sin$\frac{2}{3}x+cos\frac{2}{3}$x的图象中相邻的两条对称轴间距离为( )
| A. | $\frac{3}{2}π$ | B. | $\frac{4}{3}π$ | C. | 3π | D. | $\frac{7}{6}π$ |
18.已知不等式组$\left\{\begin{array}{l}x+y≥4\\ x-y≥-2\\ x≤2\end{array}\right.$表示的平面区域为D,点O(0,0),A(1,0).若点M是D上的动点,则$\frac{{\overrightarrow{OA}•\overrightarrow{OM}}}{{|{\overrightarrow{OM}}|}}$的最小值是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{10}}}{10}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |
15.设四边形ABCD为平行四边形,|$\overrightarrow{AB}$|=6,|$\overrightarrow{AD}$|=4,则$\overrightarrow{AC}•\overrightarrow{DB}$=( )
| A. | 10 | B. | 15 | C. | 20 | D. | 25 |
19.已知f(x)=x3-6x2+9x+2,f′(x)是f(x)的导数,f(x)和f′(x)单调性相同的区间是( )
| A. | [1,2]∪[3,+∞) | B. | [1,2]和[3,+∞) | C. | (-∞,2] | D. | [2,+∞) |
16.高一新生军训时,经过两天的打靶训练,甲每射击10次可以击中9次,乙每射击9次可以击中8次.甲、乙两人射击同一目标(甲、乙两人互不影响),现各射击一次,目标被击中的概率为( )
| A. | $\frac{9}{10}$ | B. | $\frac{4}{5}$ | C. | $\frac{8}{9}$ | D. | $\frac{89}{90}$ |