题目内容
设Sn是等差数列{an}的前n项和,已知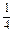 S3,
S3,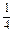 S4的等比中项为
S4的等比中项为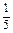 S5;
S5; 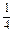 S3,
S3,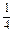 S4的等差中项为1,求数列{an}的通项公式.
S4的等差中项为1,求数列{an}的通项公式.
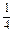 S3,
S3,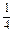 S4的等比中项为
S4的等比中项为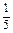 S5;
S5; 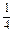 S3,
S3, S4的等差中项为1,求数列{an}的通项公式.
S4的等差中项为1,求数列{an}的通项公式.an=1或an=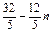
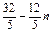
方法一 设等差数列{an}的首项a1=a,公差为d,
则Sn=na+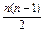 d,依题意,有
d,依题意,有
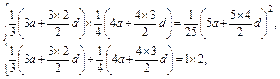
整理得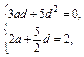
∴a=1,d=0或a=4,d=-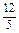 .
.
∴an=1或an=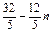 ,
,
经检验,an=1和an=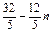 均合题意.
均合题意.
∴所求等差数列的通项公式为an=1或an=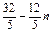 .
.
方法二 因Sn是等差数列的前n项和,易知数列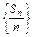 是等差数列.依题意得
是等差数列.依题意得
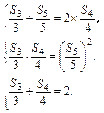 解得
解得 或
或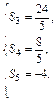
由此得a4=S4-S3=1,a5=S5-S4=1,
或a4=-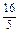 ,a5=-
,a5=-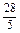 ,
,
∴d=0或d=-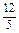 .
.
∴an=a4+(n-4)×0=1
或an=a4+(n-4)×(-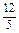 )=
)= -
-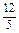 n.
n.
故所求等差数列的通项公式an=1或an= -
-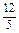 n.
n.
则Sn=na+
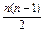 d,依题意,有
d,依题意,有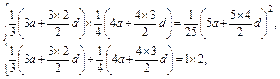
整理得
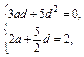
∴a=1,d=0或a=4,d=-
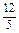 .
.∴an=1或an=
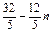 ,
,经检验,an=1和an=
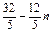 均合题意.
均合题意.∴所求等差数列的通项公式为an=1或an=
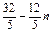 .
.方法二 因Sn是等差数列的前n项和,易知数列
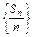 是等差数列.依题意得
是等差数列.依题意得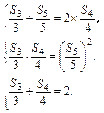 解得
解得 或
或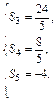
由此得a4=S4-S3=1,a5=S5-S4=1,
或a4=-
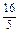 ,a5=-
,a5=-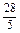 ,
,∴d=0或d=-
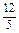 .
.∴an=a4+(n-4)×0=1
或an=a4+(n-4)×(-
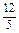 )=
)= -
-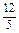 n.
n.故所求等差数列的通项公式an=1或an=
 -
-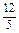 n.
n.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,已知
中,已知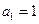 ,
, ,
, .
.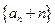 是等比数列;
是等比数列; 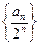 的前项和为
的前项和为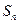 .
.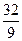 ;
;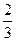 am-1,
am-1,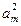 ,am+1+
,am+1+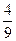 依次成等差数列.
依次成等差数列.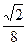 是等比数列4
是等比数列4 ,4,2
,4,2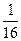 ,第二、三项的和为
,第二、三项的和为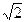 ,求这个等比数列的公比.
,求这个等比数列的公比.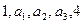 是等比数列,则
是等比数列,则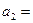 .
.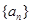 的前
的前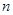 项和为
项和为 且
且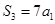 ,则数列
,则数列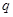 的值为()
的值为()