题目内容
是否存在一个等比数列{an},使其满足下列三个条件:
(1)a1+a6=11且a3a4=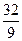 ;
;
(2)an+1>an(n∈N*);
(3)至少存在一个m(m∈N*,m>4),使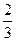 am-1,
am-1,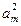 ,am+1+
,am+1+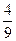 依次成等差数列.
依次成等差数列.
若存在,写出数列的通项公式;若不存在,请说明理由.
(1)a1+a6=11且a3a4=
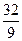 ;
;(2)an+1>an(n∈N*);
(3)至少存在一个m(m∈N*,m>4),使
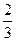 am-1,
am-1,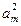 ,am+1+
,am+1+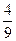 依次成等差数列.
依次成等差数列.若存在,写出数列的通项公式;若不存在,请说明理由.
∵m>4,∴不存在满足条件的等比数列.
假设存在这样的数列{an}.
∵a1+a6=11,a1a6=a3 a4=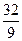 ,
,
∴a1、a6是方程x2-11x+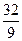 =0的两根,解得x1=
=0的两根,解得x1=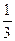 ,x2=
,x2=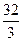 .
.
∵an+1>an(n∈N*),∴a1=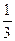 ,a6=
,a6=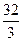 .
.
设公比为q,则a6=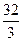 =
=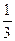 q5,于是q=2.
q5,于是q=2.
∴an=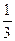 ×2n-1.
×2n-1.
由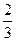 am-1,
am-1,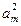 ,am+1+
,am+1+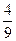 依次成等差数列,得2
依次成等差数列,得2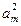 =
=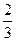 am-1+am+1+
am-1+am+1+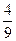 ,
,
即2×(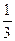 ×2m-1)2=
×2m-1)2=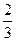 ×
×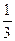 ×2m-2+
×2m-2+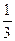 ×2m+
×2m+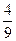 .
.
解得m=3.
又∵m>4,∴不存在满足条件的等比数列.
∵a1+a6=11,a1a6=a3 a4=
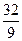 ,
,∴a1、a6是方程x2-11x+
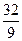 =0的两根,解得x1=
=0的两根,解得x1=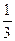 ,x2=
,x2=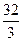 .
.∵an+1>an(n∈N*),∴a1=
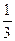 ,a6=
,a6=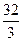 .
.设公比为q,则a6=
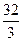 =
=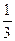 q5,于是q=2.
q5,于是q=2.∴an=
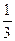 ×2n-1.
×2n-1.由
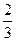 am-1,
am-1,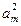 ,am+1+
,am+1+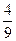 依次成等差数列,得2
依次成等差数列,得2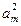 =
=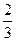 am-1+am+1+
am-1+am+1+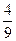 ,
,即2×(
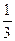 ×2m-1)2=
×2m-1)2=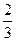 ×
×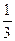 ×2m-2+
×2m-2+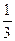 ×2m+
×2m+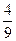 .
.解得m=3.
又∵m>4,∴不存在满足条件的等比数列.

练习册系列答案
相关题目
 (an-1).
(an-1).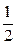
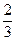 }是等比数列;
}是等比数列;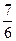 时,求数列{an}的通项公式.
时,求数列{an}的通项公式.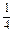 S3,
S3,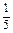 S5;
S5;  为数列
为数列 的前
的前 项和,
项和, 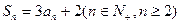 ,求数列
,求数列 列前
列前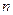 项和
项和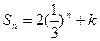 ,则常数
,则常数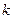 的值为 .
的值为 .