题目内容
通过直线y=x和圆x2+y2+6x=0的交点,且对称轴是坐标轴的抛物线方程是____________.
y2=-3x或x2=-3y
联立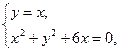
解得
交点为(0,0),(-3,-3).
所以抛物线方程为y2=-2px(p>0)或x2=-2py(p>0),将点(-3,-3)分别代入即可求得.
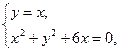解得交点为(0,0),(-3,-3).所以抛物线方程为y2=-2px(p>0)或x2=-2py(p>0),将点(-3,-3)分别代入即可求得.
练习册系列答案
黄冈冠军课课练系列答案
相关题目
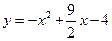，通过原点O作C的切线
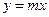，使切点P在第一象限. 
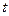，为使DOPQ的面积小于DPQR的面积，试求
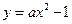的焦点是坐标原点，则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 。
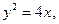F是C的焦点，过点F的直线
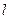与C相交于A、B两点.
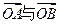夹角的大小；
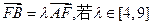，求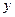
轴上截距的变化范围.
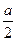,0)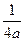
)