题目内容
(本小题满分13分)
若数列{an}的前n项和Sn是(1+x)n二项展开式中各项系数的和(n=1,2,3,……).
⑴求{an}的通项公式;
⑵若数列{bn}满足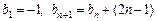 ,且
,且 ,求数列{cn}的通项及其前n项和Tn.
,求数列{cn}的通项及其前n项和Tn.
⑶求证: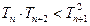 .
.
若数列{an}的前n项和Sn是(1+x)n二项展开式中各项系数的和(n=1,2,3,……).
⑴求{an}的通项公式;
⑵若数列{bn}满足
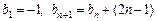 ,且
,且 ,求数列{cn}的通项及其前n项和Tn.
,求数列{cn}的通项及其前n项和Tn.⑶求证:
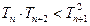 .
.(1) 由题意得 
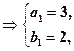
∴an=3+(n-1)=n+2.
(2)Pn==,b6=2×26-1=64. 由>64⇒n2+5n-128>0
⇒n(n+5)>128, 又n∈N*,n=9时,n(n+5)=126,
∴当n≥10时,Pn>b6.

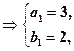
∴an=3+(n-1)=n+2.
(2)Pn==,b6=2×26-1=64. 由>64⇒n2+5n-128>0
⇒n(n+5)>128, 又n∈N*,n=9时,n(n+5)=126,
∴当n≥10时,Pn>b6.
略

练习册系列答案
相关题目
 的相邻两项
的相邻两项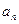 、
、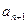 是关于
是关于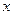 的方程
的方程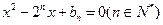 的两根,且
的两根,且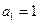 。
。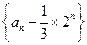 是等比数列;
是等比数列;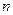 项的
项的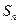 和及数列
和及数列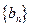 的通项公式。
的通项公式。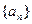 的各项均为正数,
的各项均为正数,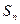 是数列
是数列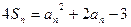 .
.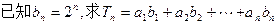 的值.
的值.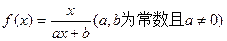 满足
满足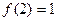 ,且
,且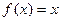 有唯一实数解。
有唯一实数解。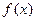 的表达式 ;
的表达式 ;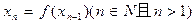 ,且
,且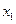 =
=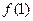 ,求数列
,求数列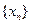 的通项公式。
的通项公式。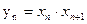 ,数列{
,数列{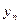 }的前
}的前 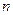 项和为
项和为 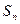 ,是否存在k∈N*,使得
,是否存在k∈N*,使得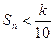 对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.
对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.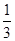 ,a2+a5=4,an=33,则n为 ( )
,a2+a5=4,an=33,则n为 ( )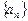 为等差数列,
为等差数列,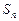 为数列
为数列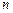 项和,已知
项和,已知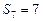 ,
,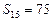 .
. 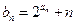 ,求数列
,求数列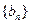 的前
的前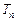 。
。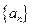 满足
满足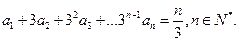
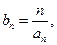 求数列
求数列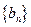 的前
的前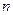 项和
项和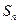 .
.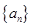 中,
中, ,则前
,则前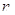 项和
项和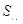 等于( )
等于( )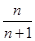
 的公比
的公比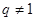 ,且
,且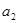 ,
,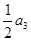 ,
,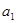 成等差数列,
成等差数列,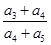 值是
值是