题目内容
【题目】已知两点![]() ,直线
,直线![]() 相交于点
相交于点![]() ,且这两条直线的斜率之积为
,且这两条直线的斜率之积为![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)记点![]() 的轨迹为曲线
的轨迹为曲线![]() ,曲线
,曲线![]() 上在第一象限的点
上在第一象限的点![]() 的横坐标为
的横坐标为![]() ,过点
,过点![]() 且斜率互为相反数的两条直线分别交曲线
且斜率互为相反数的两条直线分别交曲线![]() 于
于![]() ,求直线
,求直线![]() 的斜率(其中点
的斜率(其中点![]() 为坐标原点).
为坐标原点).
【答案】(1)![]() =
=![]() ;(2)
;(2)![]() .
.
【解析】试题分析:本题主要考查点的轨迹方程、椭圆方程、直线的方程与斜率、直线与圆锥曲线的位置关系,考查了转化思想与逻辑推理能力.(1) 设点![]() ,由题意可得
,由题意可得![]() =
=![]() ,化简可得曲线
,化简可得曲线![]() 的方程:
的方程: ![]() =
=![]() ;(2) 由题意可得点
;(2) 由题意可得点![]() ,直线
,直线![]() 与直线
与直线![]() 的斜率互为相反数,设直线
的斜率互为相反数,设直线![]() 的方程为
的方程为![]() =
= ![]() ,联立椭圆方程,由根与系数的关系式求出点P的坐标,同理求出点Q的坐标,再利用直线的斜率公式化简可得结论.
,联立椭圆方程,由根与系数的关系式求出点P的坐标,同理求出点Q的坐标,再利用直线的斜率公式化简可得结论.
试题解析:
(1)设点![]() ,
,
∵![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
整理得点所在的曲线![]() 的方程:
的方程: ![]() =
=![]() .
.
(2)由题意可得点![]() ,
,
直线![]() 与直线
与直线![]() 的斜率互为相反数,
的斜率互为相反数,
设直线![]() 的方程为
的方程为![]() =
= ![]() ,与椭圆方程联立,消去
,与椭圆方程联立,消去![]() ,
,
得: ![]() =
=![]() ,
,
由于![]() =
=![]() 是方程的一个解,
是方程的一个解,
所以方程的另一解为![]() =
=![]() ,
,
同理![]() ,
,
故直线![]() 的斜率为:
的斜率为:
![]() =
=![]() =
=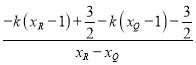 =
= =
=![]() .
.

练习册系列答案
相关题目
