题目内容
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, ![]() 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若![]() 时从区间
时从区间![]() 上任取的一个数,
上任取的一个数, ![]() 是从区间
是从区间![]() 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:由二次方程有实数根可得![]() 满足的条件
满足的条件![]() ,(Ⅰ)中由
,(Ⅰ)中由![]() 可以取得值得到所有基本事件个数及满足条件的基本事件个数,求其比值可求概率;(Ⅱ)中由
可以取得值得到所有基本事件个数及满足条件的基本事件个数,求其比值可求概率;(Ⅱ)中由![]() 范围得到
范围得到![]() 对应的区域,并求得满足
对应的区域,并求得满足![]() 的区域,求其面积比可求其概率
的区域,求其面积比可求其概率
试题解析:设事件![]() 为“方程
为“方程![]() 有实数根”.
有实数根”.
当![]() 时,因为方程
时,因为方程![]() 有实数根,
有实数根,
则![]()
(Ⅰ)基本事件共12个,如下:(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)其中第一个数表示![]() 的取值,第二个数表示
的取值,第二个数表示![]() 的取值,事件
的取值,事件![]() 包含9个基本事件,事件
包含9个基本事件,事件![]() 发生的概率为
发生的概率为![]()
(Ⅱ)实验的全部结果所构成的区域为![]() ,
,
构成事件![]() 的区域为
的区域为![]()
所以所求的概率为: 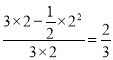

【题目】根据国家环保部最新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米。某城市环保部分随机抽取的一居民区过去20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
组别 | PM2.5平均浓度 | 频数 | 频率 |
第一组 | (0,25] | 3 | 0.15 |
第二组 | (25,50] | 12 | 0.6 |
第三组 | (50,75] | 3 | 0.15 |
第四组 | (75,100] | 2 | 0.1 |
(Ⅰ)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
(II)求样本平均数,并根据样本估计总计的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?并说明理由.