Question

【题目】对于定义在区间上的两个函数和，如果对任意的，均有不等式成立，则称函数与在上是“友好”的，否则称为“不友好”的．

（1）若，，则与在区间上是否“友好”；

（2）现在有两个函数与，给定区间．

①若与在区间上都有意义，求的取值范围；

②讨论函数与与在区间上是否“友好”．

Answer 1

【答案】（1）是；（2）①；②见解析

【解析】

（1）按照定义，只需判断在区间上是否恒成立；

（2）①由题意解不等式组即可；②假设存在实数，使得与与在区间上是“友好”的，即，即，只需求出函数在区间上的最值，解不等式组即可.

（1）由已知，，因为时，

，所以恒成立，故

与在区间上是“友好”的.

（2）①与在区间上都有意义，

则必须满足，解得，又且，

所以的取值范围为.

②假设存在实数，使得与与在区间上是“友好”的，

则，即，

因为，则，，所以在的右侧，

又复合函数的单调性可得在区间上为减函数，

从而，，

所以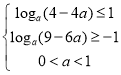，解得，

所以当时，与与在区间上是“友好”的；

当时，与与在区间上是“不友好”的.