题目内容
【题目】探究与发现:为什么二次函数![]() 的图象是抛物线?我们知道,平面内与一个定点F和一条定直线l距离相等的点的轨迹是抛物线,这是抛物线的定义,也是其本质特征
的图象是抛物线?我们知道,平面内与一个定点F和一条定直线l距离相等的点的轨迹是抛物线,这是抛物线的定义,也是其本质特征![]() 因此,只要说明二次函数的图象符合抛物线的本质特征,就解决了为什么二次函数
因此,只要说明二次函数的图象符合抛物线的本质特征,就解决了为什么二次函数![]() 的图象是抛物线的问题
的图象是抛物线的问题![]() 进一步讲,由抛物线与其方程之间的关系可知,如果能用适当的方式将
进一步讲,由抛物线与其方程之间的关系可知,如果能用适当的方式将![]() 转化为抛物线标准方程的形式,那么就可以判定二次函数
转化为抛物线标准方程的形式,那么就可以判定二次函数![]() 的图象是抛物线了.下面我们就按照这个思路来展开.对二次函数式
的图象是抛物线了.下面我们就按照这个思路来展开.对二次函数式![]() 的右边配方,得
的右边配方,得![]() .由函数图象平移
.由函数图象平移![]() 一般地,设
一般地,设![]() 是坐标平面内的一个图形,将
是坐标平面内的一个图形,将![]() 上所有点按照同一方向,移动同样的长度,得到图形
上所有点按照同一方向,移动同样的长度,得到图形![]() ,这一过程叫作图形的平移
,这一过程叫作图形的平移![]() 的知识可以知道,沿向量
的知识可以知道,沿向量![]() 平移函数
平移函数![]() 的图象
的图象![]() 如图,函数图象的形状、大小不发生任何变化,平移后图象对应的函数解析式为
如图,函数图象的形状、大小不发生任何变化,平移后图象对应的函数解析式为![]() ,我们把它改写为
,我们把它改写为![]() 的形式
的形式![]() 方程
方程![]() ,这是顶点为坐标原点,焦点为
,这是顶点为坐标原点,焦点为![]() 的抛物线.这样就说明了二次函数
的抛物线.这样就说明了二次函数![]() 的图象是一条抛物线.
的图象是一条抛物线.
请根据以上阅读材料,回答下列问题:
![]() 由函数
由函数![]() 的图象沿向量
的图象沿向量![]() 平移,得到的图象对应的函数解析式为
平移,得到的图象对应的函数解析式为![]() ,求
,求![]() 的坐标;
的坐标;
![]() 过抛物线
过抛物线![]() 的焦点F的一条直线交抛物线于P、Q两点若线段PF与QF的长分别是p、q,试探究
的焦点F的一条直线交抛物线于P、Q两点若线段PF与QF的长分别是p、q,试探究![]() 是否为定值?并说明理由.
是否为定值?并说明理由.

【答案】(1)![]() ;(2)4
;(2)4
【解析】
(1)将![]() 配方成
配方成![]() ,根据图像变换的知识,可求得
,根据图像变换的知识,可求得![]() .(2)求出抛物线的焦点坐标和准线方程,设出直线
.(2)求出抛物线的焦点坐标和准线方程,设出直线![]() 的方程,联立直线方程和抛物线的方程,消去
的方程,联立直线方程和抛物线的方程,消去![]() ,得到关于
,得到关于![]() 的一元二次方程,由此写出韦达定理,根据抛物线的定义求得
的一元二次方程,由此写出韦达定理,根据抛物线的定义求得![]() 的表达式,代入
的表达式,代入![]() 化简后可求得
化简后可求得![]() 为定值
为定值![]() .
.
解:![]() ,
,
![]() .
.
![]() 由
由![]() 可得
可得![]() ,故F
,故F![]() ,抛物线的准线方程为
,抛物线的准线方程为![]() .
.
设直线PQ的斜率为k,则直线PQ的方程为![]() ,
,
联立方程组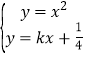 ,消去x可得:
,消去x可得:![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
由抛物线的定义可知:![]() ,
,![]() ,
,
![]() .
.
即![]() 为定值4.
为定值4.

 阅读快车系列答案
阅读快车系列答案【题目】某地区对12岁儿童瞬时记忆能力进行调查,瞬时记忆能力包括听觉记忆能力与视觉记忆能力。某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果。例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人。
视觉 听觉 | 视觉记忆能力 | ||||
偏低 | 中等 | 偏高 | 超常 | ||
听觉 记忆 能力 | 偏低 | 0 | 7 | 5 | 1 |
中等 | 1 | 8 | 3 | b | |
偏高 | 2 | a | 0 | 1 | |
超常 | 0 | 2 | 1 | 1 | |
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为![]() 。
。
(1)试确定a,b的值;
(2)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为X,求随机变量X的分布列。

