Question

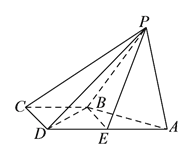
【题目】如图，在四棱锥中，平面平面，，，，，为的中点．

（）求证：．

（）求证：平面平面．

（）在平面内是否存在，使得直线平面，请说明理由．

Answer 1

【答案】（1）见解析；（2）见解析；（3）见解析

【解析】试题分析：

（1）由平面平面，可得平面，故证得．（2）先证明四边形是正方形，连结，则．又可证得四边形是平行四边形，故，可得．根据（1）得平面，故，从而可得平面，故平面平面．（3）当为直线的交点时，满足平面，根据线面平行的判定定理可证明．

试题解析：

（）证明：∵平面平面，平面平面，，

∴平面，

又平面，

∴．

（）由已知，，且，

∴四边形是平行四边形，

又，，

∴四边形是正方形，

连结，则，

又，，

∴四边形是平行四边形，

∴，

∴，

由（）知平面，平面，

∴，

又，

∴平面，

∵平面，

∴平面平面．

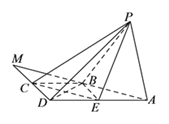
（3）当为直线的交点时，有平面．

理由如下：

在四边形中，，，

∴四边形为梯形，

∴必定相交，设交点为．

由（2）知四边形是正方形，

∴，

又 平面，平面，

∴平面．

故平面内存在，使得直线平面，且为直线的交点．