题目内容
【题目】设不等式-2<|x-1|-|x+2|<0的解集为M ,a,b∈M .
(Ⅰ)证明:|![]() |<
|<![]() ;
;
(Ⅱ)比较|1-4ab|与2|a-b|的大小,并说明理由.
【答案】(Ⅰ)证明见解析;(Ⅱ)答案见解析.
【解析】试题分析:
(1)首先求得集合M,然后结合绝对值不等式的性质即可证得题中的结论;
(2)利用平方做差的方法可证得|1-4ab|>2|a-b|.
试题解析:
(Ⅰ)证明:记f (x) =|x-1|-|x+2|,
则f(x)= 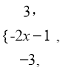
 ,所以解得-
,所以解得-![]() <x<
<x<![]() ,故M=(-
,故M=(-![]() ,
,![]() ).
).
所以,|![]() |≤
|≤![]() |a|+
|a|+![]() |b|<
|b|<![]() ×
×![]() +
+![]() ×
×![]() =
=![]() .
.
(Ⅱ)由(Ⅰ)得0≤a2<![]() ,0≤b2<
,0≤b2<![]() .
.
|1-4ab|2-4|a-b|2=(1-8ab+16a2b2)-4(a2-2ab+b2)=4(a2-1)(b2-1)>0.
所以,|1-4ab|>2|a-b|.

练习册系列答案
相关题目
【题目】海南省椰树集团引进德国净水设备的使用年限(年)和所需要的维修费用y(千元)的几组统计数据如表:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)请根据上表提供的数据,用最小二乘法求出 ![]() 关于x的线性回归方程
关于x的线性回归方程 ![]() ;
;
(2)我们把中(1)的线性回归方程记作模型一,观察散点图发现该组数据也可以用函数模型 ![]() =c1ln(c2x)拟合,记作模型二.经计算模型二的相关指数R2=0.64,
=c1ln(c2x)拟合,记作模型二.经计算模型二的相关指数R2=0.64,
①请说明R2=0.64这一数据在线性回归模型中的实际意义.
②计算模型一中的R2的值(精确到0.01),通过数据说明,两种模型中哪种模型的拟合效果好.
参考公式和数值:用最小工乘法求线性回归方程系数公式 ![]() =
=  ,
, ![]() .R2=1﹣
.R2=1﹣  ,
, ![]() =0.651,(2×2.2+3×3.8+4×5.5+5×6.5+6×7.0=112.3)
=0.651,(2×2.2+3×3.8+4×5.5+5×6.5+6×7.0=112.3)