题目内容
【题目】某校举行“庆元旦”教工羽毛球单循环比赛（任意两个参赛队伍只比赛一场），有高一、高二、高三共三个队参赛，高一胜高二的概率为
，高一胜高三的概率为
，高二胜高三的概率为
，每场胜负相互独立，胜者记1分，负者记0分，规定：积分相同时，高年级获胜.
（1）若高三获得冠军的概率为
，求
；
（2）记高三的得分为
，求
的分布列和期望.
【答案】(1) 
;(2)见解析.
【解析】【试题分析】（1）依据题设条件建立方程分析求解；（2）依据题设条件建立随机变量的概率分布，运用随机变量的数学期望计算公式分析探求：
（1）高三获得冠军有两种情况：高三胜两场；三个队各胜一场.
高三胜两场的概率为
.
三个队各胜一场的概率为
.
所以
，所以
.
（2）高三的得分
的所有可能取值为0,1,2，
， 
， 
，
所以
的分布列为：
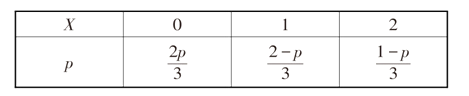
故
的期望为
.
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】某车间20名工人年龄数据如下表：
年龄（岁） | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合计 |
工人数（人） | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
（1）求这20名工人年龄的众数与平均数；
（2）以十位数为茎，个位数为叶，作出这20名工人年龄的茎叶图；
（3）从年龄在24和26的工人中随机抽取2人，求这2人均是24岁的概率.
