题目内容
【题目】海南省椰树集团引进德国净水设备的使用年限(年)和所需要的维修费用y(千元)的几组统计数据如表:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)请根据上表提供的数据,用最小二乘法求出 ![]() 关于x的线性回归方程
关于x的线性回归方程 ![]() ;
;
(2)我们把中(1)的线性回归方程记作模型一,观察散点图发现该组数据也可以用函数模型 ![]() =c1ln(c2x)拟合,记作模型二.经计算模型二的相关指数R2=0.64,
=c1ln(c2x)拟合,记作模型二.经计算模型二的相关指数R2=0.64,
①请说明R2=0.64这一数据在线性回归模型中的实际意义.
②计算模型一中的R2的值(精确到0.01),通过数据说明,两种模型中哪种模型的拟合效果好.
参考公式和数值:用最小工乘法求线性回归方程系数公式 ![]() =
=  ,
, ![]() .R2=1﹣
.R2=1﹣  ,
, ![]() =0.651,(2×2.2+3×3.8+4×5.5+5×6.5+6×7.0=112.3)
=0.651,(2×2.2+3×3.8+4×5.5+5×6.5+6×7.0=112.3)
【答案】
(1)解:∵ ![]() ,且
,且 ![]() ,∴
,∴ ![]()
![]()
∴回归直线为 ![]() .
.
(2)解:①R2=0.64表明“净水设备的使用年限解释了64%的维修费用的变化”,或者说“净水设备的维修费用
的差异有64%是由净水设备的使用年限引起的”
② ![]() ,
, ![]() ,
, 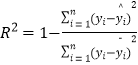 =0.96R2
=0.96R2
取值越大,意味着残差平方和越小,也就是说模型的拟合效果越好.
由于模型一中的相关指数R2=0.96大于0.64,说明模型一的拟合效果好
【解析】(1)先做出两组数据的平均数,把平均数和条件中所给的两组数据代入求解b的公式,做出b的值,再求出a的值,写出回归直线的方程.(2)①R2=0.64表明“净水设备的使用年限解释了64%的维修费用的变化”,或者说“净水设备的维修费用的差异有64%是由净水设备的使用年限引起的”②R2取值越大,意味着残差平方和越小,也就是说模型的拟合效果越好.

【题目】为了解患肺心病是否与性别有关,在某医院对入院者用简单随机抽样方法抽取50人进行调查,结果如下列联表:

(Ⅰ)是否有![]() 的把握认为入院者中患肺心病与性别有关?请说明理由;
的把握认为入院者中患肺心病与性别有关?请说明理由;
(Ⅱ)已知在患肺心病的10位女性中,有3位患胃病.现在从这10位女性中,随机选出3名进行其它方面的排查,记选出患胃病的女性人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 .
.