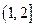题目内容
经过圆 的圆心C,且与直线
的圆心C,且与直线 垂直的直线方程是 ( )
垂直的直线方程是 ( )
 的圆心C,且与直线
的圆心C,且与直线 垂直的直线方程是 ( )
垂直的直线方程是 ( )| A.x+y+1=0 | B.x+y-1=0 | C.x-y+1=0 | D.x-y-1=0 |
C
分析:先求圆心,再求斜率,可求直线方程.
解答:解:易知点C为(-1,0),而直线与x+y=0垂直,所以待求直线的斜率为1,我们设待求的直线的方程为y=x+b,将点C的坐标代入马上就能求出参数b的值为b=1,故待求的直线的方程为x-y+1=0.
故答案为: C
点评:明确直线垂直的判定,会求圆心坐标,再求方程,是一般解题思路.
解答:解:易知点C为(-1,0),而直线与x+y=0垂直,所以待求直线的斜率为1,我们设待求的直线的方程为y=x+b,将点C的坐标代入马上就能求出参数b的值为b=1,故待求的直线的方程为x-y+1=0.
故答案为: C
点评:明确直线垂直的判定,会求圆心坐标,再求方程,是一般解题思路.

练习册系列答案
相关题目

 是圆
是圆 外一点,直线
外一点,直线 与圆
与圆 、
、 ,
, 、
、 是圆
是圆 、
、 。若
。若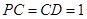 ,则四边形
,则四边形 的面积
的面积 .
.
 ,则
,则 的最大值为
的最大值为  :
: 的距离为
的距离为 .求这个圆的方程.
.求这个圆的方程. 且OC = 3,AB = 4,延长OA到D点,则△ABD的面积是___________.
且OC = 3,AB = 4,延长OA到D点,则△ABD的面积是___________.
 点是双曲线
点是双曲线 上一点,
上一点, 、
、 是它的左、右焦点,若
是它的左、右焦点,若 ,则双曲线的离心率的取值范围是
,则双曲线的离心率的取值范围是