题目内容
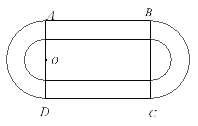
某学校要建造一个面积为10000平方米的运动场.如图，运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道，运动场除跑道外，其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元，草皮每平方米造价为30元
（1）设半圆的半径OA=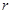
(米),试建立塑胶跑道面积S与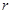的函数关系S(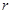) ，并求其定义域；
（2）由于条件限制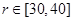
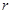,问当取何值时,运动场造价最低?（
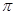取3.14）
（1）设半圆的半径OA=
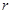(米),试建立塑胶跑道面积S与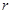的函数关系S(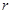) ，并求其定义域； （2）由于条件限制
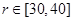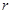,问当取何值时,运动场造价最低?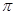（取3.14）(1)塑胶跑道面积
∵
∴
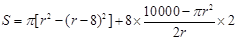
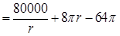
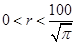，故定义域为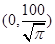
(2)设运动场的造价为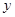
元
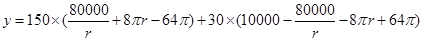
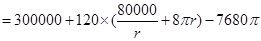
∵函数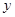
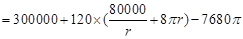在[30,40]上为减函数.
∴当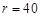
时,函数有最小值
∵
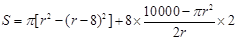
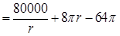
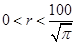∴，故定义域为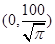(2)设运动场的造价为
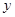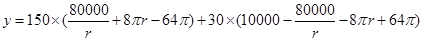
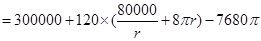
元 ∵函数
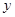
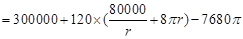在[30,40]上为减函数.∴当
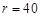时,函数有最小值 略
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
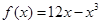在区间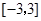
上的最小值是 ．
，（
），
与曲线
在它们的交点（1，c）处具有公共切线，求a,b的值
时，若函数
的单调区间，并求其在区间（-∞，-1）上的最大值。
，在
时有极值10，则
-
= ▲ ．
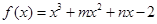的图象过点（-1，-6），且函数
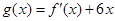的图象关于y轴对称.
、
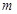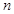的值及函数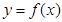
的单调区间；
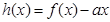在（-1，1）上单调递减，求实数
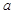的取值范围。
是常数）在[－2，2]上有最大值3，那么在[－2，2]上的最小值是 ( ▲ )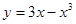
，
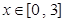的值域是__ __
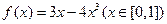的最大值是 ▲