题目内容
已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为( )
| A.-1<a<2 | B.-3<a<6 | C.a<-1或a>2 | D.a<-3或a>6 |
D
解:因为三次函数存在极大值和极小值,因此则其导函数必有两个不等的实数根,即
f‘(x)=3x2+2ax+(a+6)中判别式大于零,即为4a2-12(+6)>0,解得为a<-3或a>6

练习册系列答案
相关题目
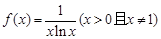 .
.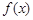 的单调区间;
的单调区间; 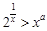 对任意
对任意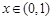 成立,求实数
成立,求实数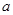 的取值范围;
的取值范围;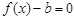 的零点个数.
的零点个数.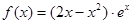 判断正确的是( )
判断正确的是( )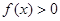 的解集是
的解集是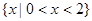 ;
;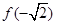 是极小值,
是极小值,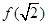 是极大值;
是极大值;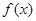 没有最小值,也没有最大值.
没有最小值,也没有最大值.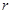 (米),试建立塑胶跑道面积S与
(米),试建立塑胶跑道面积S与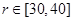 ,问当
,问当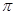 取3.14)
取3.14)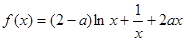 (a∈R).
(a∈R).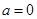 时,求
时,求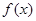 的极值;
的极值;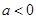 时,求
时,求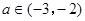 及
及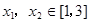 ,恒有
,恒有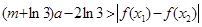
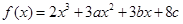 在
在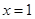 及
及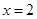 时取得极值.
时取得极值.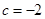 时,求函数
时,求函数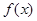 在区间
在区间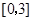 上的最大值.
上的最大值.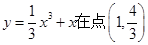 处的切线方程 。
处的切线方程 。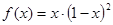 的极值点的个数是( )
的极值点的个数是( )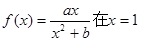 处取得极值2,则当
处取得极值2,则当