题目内容
函数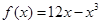 在区间
在区间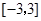 上的最小值是 .
上的最小值是 .
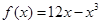 在区间
在区间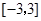 上的最小值是 .
上的最小值是 .
解:∵f'(x)=12-3x2,
∴f'(x)=0,得x=±2,
∵f(-2)=-16,f(3)=9,f(-3)=-9,f(2)=6,
∴f(x)min=f(-2)=-16.
故答案为:-16.
∴f'(x)=0,得x=±2,
∵f(-2)=-16,f(3)=9,f(-3)=-9,f(2)=6,
∴f(x)min=f(-2)=-16.
故答案为:-16.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
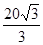
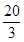
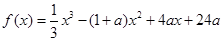 ,其中
,其中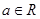 .
.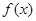 有极值,求
有极值,求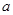 的取值范围;
的取值范围;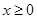 ,
,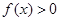 恒成立,求
恒成立,求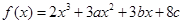 在
在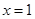 及
及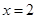 时取得极值.
时取得极值.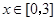 ,都有
,都有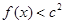 成立,求c的取值范围.
成立,求c的取值范围. 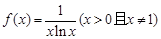 .
.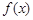 的单调区间;
的单调区间; 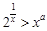 对任意
对任意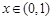 成立,求实数
成立,求实数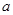 的取值范围;
的取值范围;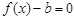 的零点个数.
的零点个数.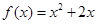 ,在使
,在使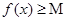 成立的所有常数
成立的所有常数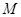 中,我们把
中,我们把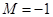 叫做
叫做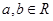 ,且
,且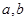 不全为
不全为 ,
,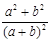 的下确界是( )
的下确界是( )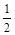
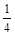
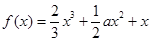 ,
,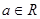 .
.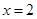 时,
时,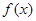 取得极值,求
取得极值,求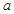 的值;
的值;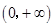 内为增函数,求
内为增函数,求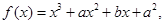
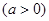 在
在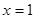 处有极值
处有极值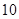 ,那么
,那么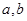 的值分别为_____ ___ 。
的值分别为_____ ___ 。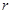 (米),试建立塑胶跑道面积S与
(米),试建立塑胶跑道面积S与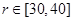 ,问当
,问当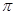 取3.14)
取3.14)