题目内容
已知函数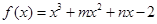 的图象过点(-1,-6),且函数
的图象过点(-1,-6),且函数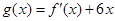 的图象关于y轴对称.
的图象关于y轴对称.
(1)求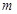 、
、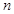 的值及函数
的值及函数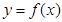 的单调区间;
的单调区间;
(2)若函数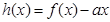 在(-1,1)上单调递减,求实数
在(-1,1)上单调递减,求实数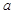 的取值范围。
的取值范围。
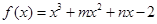 的图象过点(-1,-6),且函数
的图象过点(-1,-6),且函数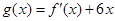 的图象关于y轴对称.
的图象关于y轴对称.(1)求
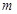 、
、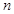 的值及函数
的值及函数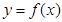 的单调区间;
的单调区间;(2)若函数
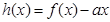 在(-1,1)上单调递减,求实数
在(-1,1)上单调递减,求实数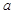 的取值范围。
的取值范围。解:(1)由函数f(x)图象过点(-1,-6),得m-n="-3,"
由f(x)=x3+mx2+nx-2,得f′(x)=3x2+2mx+n,
则g(x)=f′(x)+6x=3x2+(2m+6)x+n;
而g(x)图象关于y轴对称,所以- =0,所以m=-3,代入①得n=0.
=0,所以m=-3,代入①得n=0.
于是f′(x)=3x2-6x=3x(x-2). 由f′(x)>0得x>2或x<0,
故f(x)的单调递增区间是(-∞,0),(2,+∞);
由f′(x)<0得0<x<2,
故f(x)的单调递减区间是(0,2).
(2)解: 由 在(-1,1)上恒成立,得a≥3x2-6x对x∈(-1,1)恒成立. ∵-1<x<1,∴3x2 -6x<9,∴只需a≥9.∴a≥9.
在(-1,1)上恒成立,得a≥3x2-6x对x∈(-1,1)恒成立. ∵-1<x<1,∴3x2 -6x<9,∴只需a≥9.∴a≥9.
由f(x)=x3+mx2+nx-2,得f′(x)=3x2+2mx+n,
则g(x)=f′(x)+6x=3x2+(2m+6)x+n;
而g(x)图象关于y轴对称,所以-
 =0,所以m=-3,代入①得n=0.
=0,所以m=-3,代入①得n=0.于是f′(x)=3x2-6x=3x(x-2). 由f′(x)>0得x>2或x<0,
故f(x)的单调递增区间是(-∞,0),(2,+∞);
由f′(x)<0得0<x<2,
故f(x)的单调递减区间是(0,2).
(2)解: 由
 在(-1,1)上恒成立,得a≥3x2-6x对x∈(-1,1)恒成立. ∵-1<x<1,∴3x2 -6x<9,∴只需a≥9.∴a≥9.
在(-1,1)上恒成立,得a≥3x2-6x对x∈(-1,1)恒成立. ∵-1<x<1,∴3x2 -6x<9,∴只需a≥9.∴a≥9.本试题主要考查了导数在函数研究中的应用。利用导数能求解函数的单调性和奇偶性问题,以及能根据函数单调区间,逆向求解参数的取值范围的求解问题。要利用导数恒小于等于零来解得 。

练习册系列答案
相关题目
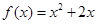 ,在使
,在使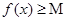 成立的所有常数
成立的所有常数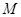 中,我们把
中,我们把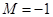 叫做
叫做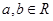 ,且
,且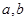 不全为
不全为 ,
,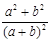 的下确界是( )
的下确界是( )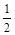
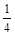
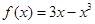 在区间
在区间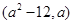 上有最小值,则实数
上有最小值,则实数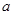 的取值范围是 .
的取值范围是 .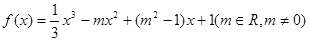 的导函数
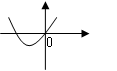
的导函数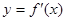 的图像如右图所示,则
的图像如右图所示,则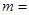 _______.
_______.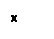
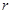 (米),试建立塑胶跑道面积S与
(米),试建立塑胶跑道面积S与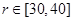 ,问当
,问当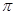 取3.14)
取3.14)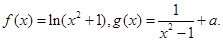
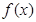 的一个极值点到直线
的一个极值点到直线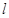 的距离为1,求
的距离为1,求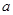 的值;
的值;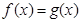 的根的个数.
的根的个数.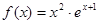 ,
,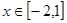 的最大值为( )
的最大值为( )


