题目内容
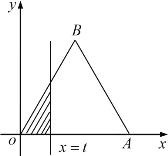
【题目】如图所示，在平面直角坐标系
中，已知椭圆
：
（
），
，
，
，
是椭圆上的四个动点，且
，
，线段
与
交于椭圆内一点
.当点
的坐标为
，且，分别为椭圆的上顶点和右顶点重合时，四边形
的面积为4.
（Ⅰ）求椭圆的标准方程；
（Ⅱ）证明：当点，，，在椭圆上运动时，
（
）是定值.
【答案】（Ⅰ）
；（Ⅱ）
是定值
【解析】
【试题分析】（1）依据题设条件建立方程组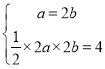
，然后解方程组求出
，
；（2）先设四点坐标分别为
，
，
，
，然后将点
，
的坐标代入椭圆方程得：
，
.再两式相减得：
，求得
，进而得到
，①
将点
，
的坐标代入椭圆方程，同理可得：
，最后设
（
），得
，即
，即
，
，②。再设
，同理可得：
，
，③。由①②③得：
，
整理得：
，进而得到
，从而求出
。
解：（Ⅰ）由题可知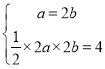：，解得，，
所以椭圆
的标准方程
.
（Ⅱ）设，，，，
将点，的坐标代入椭圆方程得：，.
两式相减得：，
∵，∴，①
将点，的坐标代入椭圆方程，同理可得：，
设（），得，
即，即，，②
设，同理可得：，，③
由①②③得： ，
整理得： ，
即，
∵
，
，∴，
所以
是定值.
练习册系列答案
相关题目
【题目】某商场周年庆，准备提供一笔资金，对消费满一定金额的顾客以参与活动的方式进行奖励.顾客从一个装有大小相同的2个红球和4个黄球的袋中按指定规则取出2个球，根据取到的红球数确定奖励金额，具体金额设置如下表：
取到的红球数 | 0 | 1 | 2 |
奖励（单位：元） | 5 | 10 | 50 |
现有两种取球规则的方案：
方案一：一次性随机取出2个球；
方案二：依次有放回取出2个球.
（Ⅰ）比较两种方案下，一次抽奖获得50元奖金概率的大小；
（Ⅱ）为使得尽可能多的人参与活动，作为公司的负责，你会选择哪种方案？请说明理由.
