题目内容
【题目】设椭圆![]() 的左顶点为
的左顶点为![]() ,右顶点为
,右顶点为![]() .已知椭圆的离心率为
.已知椭圆的离心率为![]() ,且以线段
,且以线段![]() 为直径的圆被直线
为直径的圆被直线![]() 所截得的弦长为
所截得的弦长为![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() ,且点
,且点![]() 在第一象限,点
在第一象限,点![]() 关于
关于![]() 轴对称点为点
轴对称点为点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,若直线
,若直线![]() 斜率大于
斜率大于![]() ,求直线
,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
(Ⅰ)利用直线被圆截得弦长为![]() 构造关于
构造关于![]() 的方程,求得
的方程,求得![]() ,再根据离心率和
,再根据离心率和![]() 之间关系求得
之间关系求得![]() ,从而得到椭圆方程;(Ⅱ)假设
,从而得到椭圆方程;(Ⅱ)假设![]() ,则
,则![]() ,表示出直线
,表示出直线![]() 和直线
和直线![]() ,求解出
,求解出![]() 点坐标,从而利用直线
点坐标,从而利用直线![]() 斜率大于
斜率大于![]() ,求得
,求得![]() ;又
;又![]() 为椭圆上的点且在第一象限,可知
为椭圆上的点且在第一象限,可知![]() ,从而可得
,从而可得![]() ;将
;将![]() 表示为关于
表示为关于![]() 的函数,利用函数求值域的方法求解出
的函数,利用函数求值域的方法求解出![]() 的取值范围.
的取值范围.
(Ⅰ)以线段![]() 为直径的圆的圆心为:
为直径的圆的圆心为:![]() ,半径
,半径![]()
![]() 圆心到直线
圆心到直线![]() 的距离
的距离![]()
![]() 直线
直线![]() 被圆截得的弦长为
被圆截得的弦长为![]()
解得:![]() ,又椭圆离心率
,又椭圆离心率![]()
![]() ,
,![]()
![]() 椭圆的标准方程为:
椭圆的标准方程为:![]()
(Ⅱ)设![]() ,其中
,其中![]() ,
,![]() ,则
,则![]()
![]() ,
,![]()
则直线![]() 为:
为:![]() ;直线
;直线![]() 为:
为:![]()
由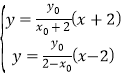 得:
得:![]()
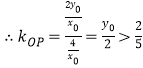
![]()
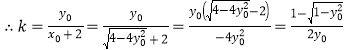
令![]() ,
,![]() ,则
,则![]()
![]()
![]()
![]()
![]()
即![]()

练习册系列答案
相关题目