题目内容
19.解答下列问题:(1)已知角α∈(π,2π),且cos(α-11π)=-$\frac{3}{5}$,求tan(α-9π)的值;
(2)求sin(-660°)-cos420°-tan330°•tan(-690°)的值.
分析 利用三角函数的诱导公式分别化简求值:奇变偶不变,符号看象限.
解答 解:(1)因为α∈(π,2π),且cos(α-11π)=cos(π-α)=-cosα=-$\frac{3}{5}$,
所以cos$α=\frac{3}{5}$,sinα=$-\frac{4}{5}$,
所以tan(α-9π)=tanα=$\frac{sinα}{cosα}$=$-\frac{4}{3}$;
(2)sin(-660°)-cos420°-tan330°•tan(-690°)
=sin(-720°+60°)-cos(360°+60°)-tan(360°-30°)tan(-720°+30°)
=sin60°-cos60°+tan30°tan30°
=$\frac{\sqrt{3}}{2}-\frac{1}{2}+\frac{\sqrt{3}}{3}×\frac{\sqrt{3}}{3}$
=$\frac{\sqrt{3}}{2}-\frac{1}{6}$.
点评 本题考查了利用商数的诱导公式化简三角函数式;关键是熟练正确的运用诱导公式.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
7.数列{an}中,已知a1=1,a2=2,an+2=an+1-an(n∈N*),则a2015=( )
| A. | 1 | B. | -1 | C. | -2 | D. | 2 |
11.如图所示,表示阴影部分的二元一次不等式组是( )
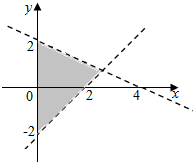

| A. | $\left\{\begin{array}{l}x-y-2<0\\ x+2y-4>0\\ x≥0\end{array}\right.$ | B. | $\left\{\begin{array}{l}x-y-2<0\\ x+2y-4<0\\ x≥0\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x-y-2>0\\ x+2y-4<0\\ x≥0\end{array}\right.$ | D. | $\left\{\begin{array}{l}x-y-2>0\\ x+2y-4>0\\ x≥0\end{array}\right.$ |
9.将一颗均匀骰子掷两次,不能作为随机变量的是( )
| A. | 两次出现的点数之和 | B. | 两次掷出的最大点数 | ||
| C. | 第一次减去第二次的点数差 | D. | 抛掷的次数 |
 如图,$|\overrightarrow{AO}|=1$,P是以AB为直径的半圆弧上的动点,以CP为一边作正△CPD,则$|\overrightarrow{OD}|$的最大值是4.
如图,$|\overrightarrow{AO}|=1$,P是以AB为直径的半圆弧上的动点,以CP为一边作正△CPD,则$|\overrightarrow{OD}|$的最大值是4.