题目内容
1.已知数列{an}中,a3=2,a7=1,且数列{$\frac{1}{{{a_n}+1}}$}为等差数列,则a8=( )| A. | -$\frac{7}{11}$ | B. | $\frac{13}{11}$ | C. | $\frac{11}{13}$ | D. | -$\frac{5}{7}$ |
分析 通过a3=2、a7=1计算出数列{$\frac{1}{{{a_n}+1}}$}的公差d,利用$\frac{1}{{a}_{8}+1}$=$\frac{1}{{a}_{7}+1}$+d,计算即得结论.
解答 解:∵a3=2,a7=1,
∴$\frac{1}{{a}_{3}+1}$=$\frac{1}{3}$,$\frac{1}{{a}_{7}+1}$=$\frac{1}{2}$,
又∵数列{$\frac{1}{{{a_n}+1}}$}为等差数列,
∴数列{$\frac{1}{{{a_n}+1}}$}的公差d=$\frac{1}{4}$($\frac{1}{{a}_{7}+1}$-$\frac{1}{{a}_{3}+1}$)=$\frac{1}{4}$($\frac{1}{2}$-$\frac{1}{3}$)=$\frac{1}{24}$,
∴$\frac{1}{{a}_{8}+1}$=$\frac{1}{{a}_{7}+1}$+d=$\frac{1}{2}$+$\frac{1}{24}$=$\frac{13}{24}$,
∴a8=$\frac{24}{13}$-1=$\frac{11}{13}$,
故选:C.
点评 本题考查等差数列的概念,注意解题方法的积累,属于基础题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
11.如图所示,表示阴影部分的二元一次不等式组是( )
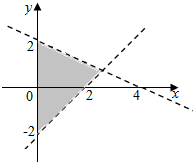

| A. | $\left\{\begin{array}{l}x-y-2<0\\ x+2y-4>0\\ x≥0\end{array}\right.$ | B. | $\left\{\begin{array}{l}x-y-2<0\\ x+2y-4<0\\ x≥0\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x-y-2>0\\ x+2y-4<0\\ x≥0\end{array}\right.$ | D. | $\left\{\begin{array}{l}x-y-2>0\\ x+2y-4>0\\ x≥0\end{array}\right.$ |
9.将一颗均匀骰子掷两次,不能作为随机变量的是( )
| A. | 两次出现的点数之和 | B. | 两次掷出的最大点数 | ||
| C. | 第一次减去第二次的点数差 | D. | 抛掷的次数 |
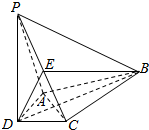 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.