题目内容
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直(其中
垂直(其中![]() 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求![]() 的解析式及单调递减区间;
的解析式及单调递减区间;
(Ⅱ)若函数![]() 无零点,求
无零点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)单调减区间为![]() 和
和![]() ;(Ⅱ)
;(Ⅱ) ![]() 的取值范围为:
的取值范围为: ![]() 或
或![]() .
.
【解析】试题分析:
(Ⅰ)利用切线求出参数![]() 值为2,解不等式
值为2,解不等式![]() 可得减区间;
可得减区间;
(Ⅱ)函数![]() 无零点,即方程
无零点,即方程![]() 在
在![]() 内无解,亦即要
内无解,亦即要![]() 在
在![]() 内无解.为此构造函数
内无解.为此构造函数![]() ,利用导数研究
,利用导数研究![]() 的单调性,可得结论,注意对
的单调性,可得结论,注意对![]() 分类讨论
分类讨论
试题解析:
(Ⅰ)解:![]() ,
,
又由题意有:![]()
![]() ,故
,故![]() .
.
此时,![]() ,由
,由![]() 或
或![]() ,
,
所以函数![]() 的单调减区间为
的单调减区间为![]() 和
和![]() .
.
(Ⅱ)解:
![]()
![]() ,且定义域为
,且定义域为![]() ,
,
要函数![]() 无零点,即要
无零点,即要![]() 在
在![]() 内无解,
内无解,
亦即要![]() 在
在![]() 内无解.
内无解.
构造函数![]() .
.
①当![]() 时,
时,![]() 在
在![]() 内恒成立,所以函数
内恒成立,所以函数![]() 在
在![]() 内单调递减,
内单调递减,![]() 在
在![]() 内也单调递减.又
内也单调递减.又![]() ,所以在
,所以在![]() 内无零点,
内无零点,
在![]() 内也无零点,故满足条件;
内也无零点,故满足条件;
②当![]() 时,
时,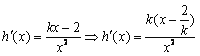
⑴若![]() ,则函数
,则函数![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内也单调递减,在
内也单调递减,在![]() 内单调递增.又
内单调递增.又![]() ,所以在
,所以在![]() 内无零点;易知
内无零点;易知![]() ,而
,而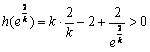 ,故在
,故在![]() 内有一个零点,所以不满足条件;
内有一个零点,所以不满足条件;
⑵若![]() ,则函数
,则函数![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内单调递增.又
内单调递增.又![]() ,所以
,所以![]() 时,
时,![]() 恒成立,故无零点,满足条件;
恒成立,故无零点,满足条件;
⑶若![]() ,则函数
,则函数![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内单调递增,在
内单调递增,在![]() 内也单调递增.又
内也单调递增.又![]() ,所以在
,所以在![]() 及
及![]() 内均无零点.
内均无零点.
又易知![]() ,而
,而![]() ,又易证当
,又易证当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 内有一零点,故不满足条件.
内有一零点,故不满足条件.
综上可得:![]() 的取值范围为:
的取值范围为:![]() 或
或![]() .
.

【题目】某化工厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料,生产1扯皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如表所示:
| A | B | C |
甲 | 4 | 8 | 3 |
乙 | 5 | 5 | 10 |
现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车品乙种肥料,产生的利润为3万元、分别用x,y表示计划生产甲、乙两种肥料的车皮数.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲、乙两种肥料,求出此最大利润.
【题目】为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:
![]()
| 应该取消 | 应该保留 | 无所谓 | |
在校学生 | 2100人 | 120人 | y人 | |
社会人士 | 600人 | x人 | z人 |
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.05.
(1)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.