题目内容
【题目】在四边形ABCD中，已知AB=9，BC=6， 
=2 
．
（1）若四边形ABCD是矩形，求 
的值；
（2）若四边形ABCD是平行四边形，且 =6，求 
与 
夹角的余弦值．
【答案】
（1）解：∵四边形ABCD是矩形，
∴ 
，即 
=0，
又AB=9，BC=6， 
=2 
，
∴| |=6，| 
|=3，
∵ 
= 
，
= 
，
∴ 
=（ ）（ ）
= 
=62﹣ 
92=18
（2）解：设 
与 
夹角为θ，由（1）得，
=（ ）（ ）
=
=62﹣ 
cosθ﹣ 92=6，
∴cosθ= 
．
【解析】（1）由条件求出| |=6，| |=3，再用向量AB，AD表示向量AP，BP，再将数量积 
展开，运用向量的平方为模的平方以及 =0，即可求出结果；（2）设 与 夹角为θ，根据得到的数量积 ，运用数量积定义，代入数据，即可求出cosθ．
【考点精析】本题主要考查了数量积表示两个向量的夹角的相关知识点，需要掌握设
、
都是非零向量，
，
，
是与
的夹角，则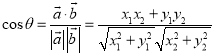
才能正确解答此题．
练习册系列答案
相关题目
