题目内容
【题目】下列命题中错误的是（ ）
A. 如果平面
不垂直于平面
，那么平面
内一定不存在直线垂直于平面
B. 如果平面
平面
，平面
平面
， 
，那么
平面
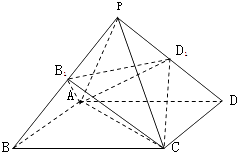
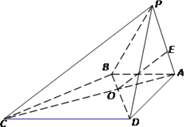
C. 不存在四个角都是直角的空间四边形
D. 空间图形经过中心投影后，直线还是直线，但平行直线可能变成相交的直线
【答案】D
【解析】选项A, 假若平面α内存在直线垂直于平面β，根据面面垂直的判定定理可知两平面垂直．故此命题成立；
选项B, 由面面垂直的性质可以分别在α、β内作异于l的直线垂直于交线，再由线面垂直的性质定理可知所作的垂线平行，进而得到线面平行再由线面平行的性质可知所作的直线与l平行，又∵两条平行线中的一条垂直于平面那么另一条也垂直于平面，故命题成立；
选项C,假设存在四个角都是直角的空间四边形A-BCD,则
AD为AB,CD的公垂线, 
BC为AB,CD的公垂线,这与公垂线的性质矛盾,故命题正确;
选项D, 空间图形经过中心投影后，直线是直线或者点，平行直线投影后可能是平行直线，重合直线，或者是两个点，不可能相交,命题错误;
故选D.
练习册系列答案
相关题目
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量（
吨）与相应的生产能耗
（吨）标准煤的几组对照数据：
|
|
|
|
|
|
|
|
|
|
（1）请画出上表数据的散点图；并指出
是否线性相关；
（2）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程
；
（3）已知该厂技术改造前
吨甲产品能耗为
吨标准煤，试根据求出的线性回归方程，预测生产
吨甲产品的生产能耗比技术改造前降低多少吨标准煤？
（参考:用最小二乘法求线性回归方程系数公式 ，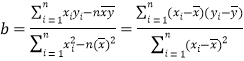
, 
.