题目内容
【题目】已知椭圆![]() 经过点
经过点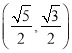 ,离心率为
,离心率为![]() ,点
,点![]() 坐标原点.
坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 的左焦点
的左焦点![]() 任作一条不垂直于坐标轴的直线
任作一条不垂直于坐标轴的直线![]() ,交椭圆
,交椭圆![]() 于
于![]() 两点,记弦
两点,记弦![]() 的中点为
的中点为![]() ,过
,过![]() 作
作![]() 的垂线
的垂线![]() 交直线
交直线![]() 于点
于点![]() ,证明:点
,证明:点![]() 在一条定直线上.
在一条定直线上.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)根据已知列式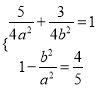 ,可求解.
,可求解.
(2) 联立![]() 与
与![]() 得
得![]() 中点
中点![]() 坐标,求得直线
坐标,求得直线![]() ,再联立方程组
,再联立方程组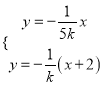 ,可得
,可得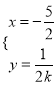 ,所以点
,所以点![]() 在定直线
在定直线![]() 上.
上.
试题解析:(1)因为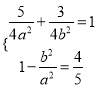 ,所以
,所以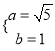 ,从而
,从而![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,联立
,联立![]() 与
与![]() ,可得
,可得![]() ,所以
,所以![]() ,设
,设![]() ,则
,则![]() ,所以
,所以![]() ,直线
,直线![]() ,联立方程组
,联立方程组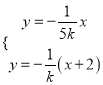 ,解得
,解得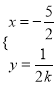 ,所以点
,所以点![]() 在定直线
在定直线![]() 上.
上.
点睛:定点、定值问题通常是通过设参数或取特殊值来确定“定点”是什么、“定值”是多少,或者将该问题涉及的几何式转化为代数式或三角问题,证明该式是恒定的. 定点、定值问题同证明问题类似,在求定点、定值之前已知该值的结果,因此求解时应设参数,运用推理,到最后必定参数统消,定点、定值显现.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目