题目内容
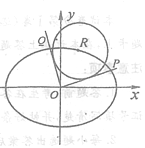
【题目】已知椭圆
的离心率为
，椭圆的左焦点为
，椭圆上任意点到的最远距离是
，过直线
与
轴的交点
任作一条斜率不为零的直线
与椭圆交于不同的两点
、
，点关于轴的对称点为
.
(1)求椭圆的方程；
(2)求证：、、三点共线；
(3)求
面积
的最大值.
【答案】(Ⅰ)
；(Ⅱ)证明见解析；(Ⅲ)
.
【解析】
(Ⅰ)由题意得到关于a,b,c的方程组，求得a,b的值即可确定椭圆方程；
(Ⅱ)设直线
的方程为
，联立直线方程与椭圆方程，结合韦达定理证明
即可证得题中的结论.
(Ⅲ)由题意可得
的面积
，结合均值不等式的结论确定面积的最大值即可.
(Ⅰ)由题意可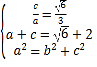得：
，解得：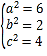
，
故椭圆的离心率为：.
(Ⅱ)结合(Ⅰ)中的椭圆方程可得：
，故
，
设直线的方程为，
联立直线方程与椭圆方程：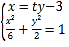
可得：
.
直线与椭圆相交，则：
，
解得：
或
.
设
，
，
则：
,
故：
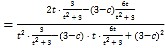
将
代入上式可得：，
故
三点共线；
(Ⅲ)结合(Ⅱ)中的结论可得：
的面积
.
当且仅当
时等号成立，故的面积的最大值为.
练习册系列答案
阅读快车系列答案
相关题目
【题目】美国制裁中兴，未来7年一颗芯片都不卖，这却激发了中国“芯”的研究热潮.某公司甲，乙，丙三个研发小组分别研发
，
，
三种不同的芯片，现在用分层抽样的方法从这些芯片中抽取若干件进行质量分析，有关数据见下表（单位：件）.
芯片 | 数量 | 抽取件数 |
| 200 |
|
| 600 |
|
| 400 | 2 |
（Ⅰ）求
的值；
（Ⅱ）若在这抽出的样品中随机抽取2件送往某机构进行进一步检测，求这2件芯片来自不同种类的概率.
