题目内容
9.设集合A={x|x2-x-2≤0},B={x|x≥a+1},若A?B,则a的取值范围是( )| A. | a<2 | B. | a≥-2 | C. | a≤-2 | D. | a>2 |
分析 由集合A={x|x2-x-2≤0}={x|-1≤x≤2},B={x|x≥a+1},A?B,结合数轴即可得出.
解答  解:∵集合A={x|x2-x-2≤0}={x|-1≤x≤2},B={x|x≥a+1},A?B,
解:∵集合A={x|x2-x-2≤0}={x|-1≤x≤2},B={x|x≥a+1},A?B,
∴a+1≤-1.
∴a≤-2,
故选:C.
点评 本题考查了集合之间的关系、数形结合的思想方法,属于基础题.

练习册系列答案
相关题目
14.一个几何体的三视图如图所示,则这个几何体的体积为( )
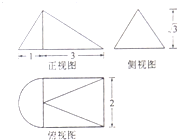

| A. | $\frac{(8+π)\sqrt{3}}{6}$ | B. | $\frac{(12+π)\sqrt{3}}{6}$ | C. | $\frac{(12+π)\sqrt{3}}{2}$ | D. | $\frac{(6+π)\sqrt{3}}{3}$ |
18.圆x2+y2-2x+4y+3=0的圆心坐标为( )
| A. | (-2,4) | B. | (2,-4) | C. | (1,-2) | D. | (-1,2) |
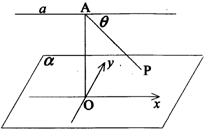 如图,已知直线a∥平面α,在平面α内有一动点P,点A是直线a上一定点,且AP与直线a所成角θ=$\frac{π}{4}$,点A到平面α的距离为2,若过点A作AO⊥α于点O,在平面α内,以过点O作直线a的平行线为x轴,以过点O作x轴的垂线为y轴建立直角坐标系,则动点P的轨迹方程为x2-y2=4..
如图,已知直线a∥平面α,在平面α内有一动点P,点A是直线a上一定点,且AP与直线a所成角θ=$\frac{π}{4}$,点A到平面α的距离为2,若过点A作AO⊥α于点O,在平面α内,以过点O作直线a的平行线为x轴,以过点O作x轴的垂线为y轴建立直角坐标系,则动点P的轨迹方程为x2-y2=4..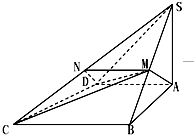 如图,四棱锥S-ABCD中,SA⊥底面ABCD,AB⊥AD,AD∥BC,SA=AB=BC=4,AD=2,M为SB的中点.
如图,四棱锥S-ABCD中,SA⊥底面ABCD,AB⊥AD,AD∥BC,SA=AB=BC=4,AD=2,M为SB的中点.