题目内容
5.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦距为4,离心率e=$\frac{{\sqrt{6}}}{3}$.(I)求椭圆C的标准方程.
(Ⅱ)设F为椭圆C的右焦点,M为直线x=3上任意一点,过F作MF的垂线交椭圆C于点A,B,N为线段AB的中点,
①证明:O、N、M三点共线(其中O为坐标原点);
②求 $\frac{{|{MF}|}}{{|{AB}|}}$的最小值及取得最小值时点M的坐标.
分析 (I)由椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦距为4,离心率e=$\frac{{\sqrt{6}}}{3}$,及a2=b2+c2,求得a2,b2,即可求椭圆C的标准方程.
(Ⅱ)①设M(3,m),A(x1,y1),B(x2,y2),AB的中点为N(x0,y0),kMF=m,设直线AB的方程为x=-my-2,代入椭圆方程,运用韦达定理和中点坐标公式,结合三点共线的方法:斜率相等,即可得证
②利用两点间距离公式及弦长公式将$\frac{{|{MF}|}}{{|{AB}|}}$表示出来,由 $\frac{{|{MF}|}}{{|{AB}|}}$取最小值时的条件获得等量关系,从而确定点T的坐标.
解答 (I)解:∵椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦距为4,离心率e=$\frac{{\sqrt{6}}}{3}$,
∴c=2,$\frac{c}{a}$=$\frac{{\sqrt{6}}}{3}$,
∴a=$\sqrt{6}$,
∴b=$\sqrt{2}$,
∴椭圆C的标准方程为$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1$.
(Ⅱ)设M(3,m),A(x1,y1),B(x2,y2),AB的中点为N(x0,y0),kMF=m
①证明:由F(2,0),可设直线AB的方程为x=-my-2,
代入椭圆方程可得(m2+3)y2-4my-2=0,
∴y1+y2=$\frac{4m}{{m}^{2}+3}$,y1y2=-$\frac{2}{{m}^{2}+3}$
于是N($\frac{6}{{m}^{2}+3}$,$\frac{2m}{{m}^{2}+3}$),则直线ON的斜率kON=$\frac{m}{3}$,
又kOM=$\frac{m}{3}$,
∴kOM=kON,
∴O,N,N三点共线
②由两点间距离公式得|MF|=$\sqrt{{m}^{2}+1}$,
由弦长公式得|PQ|=$\sqrt{{m}^{2}+1}$•|y1-y2|=$\frac{\sqrt{24}({m}^{2}+1)}{{m}^{2}+3}$,
∴$\frac{{|{MF}|}}{{|{AB}|}}$=$\frac{{m}^{2}+3}{2\sqrt{6}•\sqrt{{m}^{2}+1}}$,
令x=$\sqrt{{m}^{2}+1}$(x≥1),
则$\frac{{|{MF}|}}{{|{AB}|}}$=$\frac{{x}^{2}+2}{2\sqrt{6}x}$=$\frac{1}{2\sqrt{6}}$(x+$\frac{2}{x}$)≥$\frac{\sqrt{3}}{3}$(当且仅当x2=2时,取“=”号),
∴当$\frac{{|{MF}|}}{{|{AB}|}}$最小时,由x2=2=m2+1,得m=1或m=-1,此时点T的坐标为(-3,1)或(-3,-1).
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率和方程的运用,注意联立直线方程,运用韦达定理和中点坐标公式,同时考查三点共线的方法:斜率相等,属于中档题.

| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |
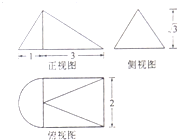
| A. | $\frac{(8+π)\sqrt{3}}{6}$ | B. | $\frac{(12+π)\sqrt{3}}{6}$ | C. | $\frac{(12+π)\sqrt{3}}{2}$ | D. | $\frac{(6+π)\sqrt{3}}{3}$ |
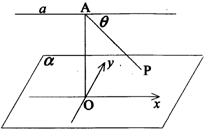 如图,已知直线a∥平面α,在平面α内有一动点P,点A是直线a上一定点,且AP与直线a所成角θ=$\frac{π}{4}$,点A到平面α的距离为2,若过点A作AO⊥α于点O,在平面α内,以过点O作直线a的平行线为x轴,以过点O作x轴的垂线为y轴建立直角坐标系,则动点P的轨迹方程为x2-y2=4..
如图,已知直线a∥平面α,在平面α内有一动点P,点A是直线a上一定点,且AP与直线a所成角θ=$\frac{π}{4}$,点A到平面α的距离为2,若过点A作AO⊥α于点O,在平面α内,以过点O作直线a的平行线为x轴,以过点O作x轴的垂线为y轴建立直角坐标系,则动点P的轨迹方程为x2-y2=4..