题目内容
15.函数f(x)是定义在R上的奇函数,且f(1)=0,当x>0时,有$\frac{xf′(x)-f(x)}{{x}^{2}}$>0恒成立,则不等式f(x)>0的解集为( )| A. | (-1,0)∪(1,+∞) | B. | (-1,0)∪(0,1) | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
分析 构造新函数g(x)=$\frac{f(x)}{x}$,得到函数g(x)的单调性,结合函数的奇偶性得到函数g(x)的图象,从而求出不等式的解集.
解答 解:令g(x)=$\frac{f(x)}{x}$,则g′(x)=$\frac{xf′(x)-f(x)}{{x}^{2}}$,
由题意知g(x)=$\frac{f(x)}{x}$在(0,+∞)上是增函数,且g(1)=0,
∵f(x)是R上的奇函数,
∴g(x)是R上的偶函数.
$\frac{f(x)}{x}$的草图如图所示: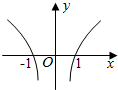
由图象知:当x>1时,f(x)>0,
当-1<x<0时,f(x)>0.
∴不等式f(x)>0的解集为(-1,0)∪(1,+∞).
点评 本题考查了函数的单调性,函数的奇偶性,考查导数的应用,构造函数g(x)是解答本题的关键,本题是一道中档题.

练习册系列答案
相关题目
5.函数f(x)=$\frac{1}{\sqrt{lo{g}_{\frac{1}{2}}({x}^{2}+2x+1)}}$的定义域为( )
| A. | (-2,0) | B. | (-2,-1)∪(-1,0) | C. | (-∞,-2)∪(0,+∞) | D. | (0,+∞) |
3.下列命题中,正确的是( )
| A. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$|⇒$\overrightarrow{a}$=$\overrightarrow{b}$ | B. | |$\overrightarrow{a}$|>|$\overrightarrow{b}$|⇒$\overrightarrow{a}$>$\overrightarrow{b}$ | C. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$|⇒$\overrightarrow{a}$∥$\overrightarrow{b}$ | D. | |$\overrightarrow{a}$|=0⇒$\overrightarrow{a}$=$\overrightarrow{0}$ |
4.下面四个图象中,有一个是函数f(x)=$\frac{1}{3}$x3+ax2+(a2-1)x+1(a∈R)的导函数y=f'(x)的图象,则f(-1)等于( )
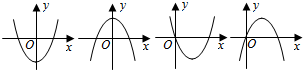
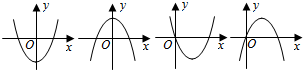
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{5}{3}$ | D. | -$\frac{1}{3}$或$\frac{5}{3}$ |