题目内容
5.函数f(x)=$\frac{1}{\sqrt{lo{g}_{\frac{1}{2}}({x}^{2}+2x+1)}}$的定义域为( )| A. | (-2,0) | B. | (-2,-1)∪(-1,0) | C. | (-∞,-2)∪(0,+∞) | D. | (0,+∞) |
分析 根据对数函数的定义域,二次根式的性质得到不等式,解出即可.
解答 解:∵${log}_{\frac{1}{2}}^{{(x}^{2}+2x+1)}$>0,
∴0<x2+2x+1<1,
即0<(x+1)2<1,
∴-2<x<0且x≠-1,
故选:B.
点评 本题考查了对数函数、二次根式的性质,是一道基础题.

练习册系列答案
相关题目
13.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线的方程是y=$\sqrt{3}$x,它的一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程是( )
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 | B. | $\frac{x^2}{3}-\frac{y^2}{8}=1$ | C. | $\frac{x^2}{6}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{8}-\frac{y^2}{16}=1$ |
20.在直角坐标系中,A(-2,3),B(3,-2),沿x轴把直角坐标系折成120°的二面角,则AB的长度为( )
| A. | $\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{11}$ |
17.已知平面向量$\overrightarrow a$=(x,-2),$\overrightarrow b$=(4,-2),$\overrightarrow a$与$\overrightarrow b$垂直,则x是( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
15.函数f(x)是定义在R上的奇函数,且f(1)=0,当x>0时,有$\frac{xf′(x)-f(x)}{{x}^{2}}$>0恒成立,则不等式f(x)>0的解集为( )
| A. | (-1,0)∪(1,+∞) | B. | (-1,0)∪(0,1) | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
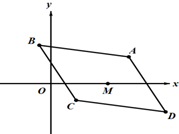 如图,平行四边形ABCD(A,B,C,D按逆时针顺序排列),AB,AD边所在直线的方程分别是x+4y-7=0,3x+2y-11=0,且对角线AC和BD的交点为M(2,0)
如图,平行四边形ABCD(A,B,C,D按逆时针顺序排列),AB,AD边所在直线的方程分别是x+4y-7=0,3x+2y-11=0,且对角线AC和BD的交点为M(2,0)