题目内容
【题目】某工厂生产某种型号的电视机零配件，为了预测今年
月份该型号电视机零配件的市场需求量，以合理安排生产，工厂对本年度
月份至
月份该型号电视机零配件的销售量及销售单价进行了调查，销售单价
（单位：元）和销售量
（单位：千件）之间的组数据如下表所示：
月份 |
|
|
|
|
|
|
销售单价 |
|
|
|
|
|
|
销售量 |
|
|
|
|
|
|
（1）根据1至月份的数据，求关于的线性回归方程（系数精确到
）；
（2）结合（1）中的线性回归方程，假设该型号电视机零配件的生产成本为每件
元，那么工厂如何制定月份的销售单价，才能使该月利润达到最大（计算结果精确到
）？
参考公式：回归直线方程
，其中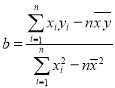
.
参考数据：
.
【答案】（1）
（2）7月份销售单价为10.8元时，该月利润才能达到最大.
【解析】
（1）利用公式可计算线性回归方程.
（2）利用（1）的回归方程可得7月份的利润函数，利用二次函数的性质可得其最大值.
解:（1）由条件知，
，
，
，
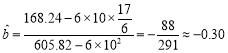从而
，
故
关于
的线性回归方程为.
（2）假设7月份的销售单价为元，则由（1）可知，7月份零配件销量为，
故7月份的利润
，
其对称轴
，故7月份销售单价为10.8元时，该月利润才能达到最大.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】为考察高中生的性别与是否喜欢数学课程之间的关系，某校在高中生中随机抽取100名学生进行了问卷调查，得到如下列联表：
喜欢数学 | 不喜欢数学 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 50 | 100 |
（1）请将上面的列联表补充完整；
（2）能否在犯错误的概率不超过0.001的前提下认为“喜欢数学”与性别有关？说明你的理由；
（3）若在接受调查的所有男生中按照“是否喜欢数学”进行分层抽样，现随机抽取6人，再从6人中抽取3人，求至少有1人“不喜欢数学”的概率.
下面的临界值表供参考：
| 0.05 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 6.635 | 7.879 | 10.828 |
（参考公式：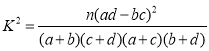
，其中
）.
【题目】在一次考试中，某班级50名学生的成绩统计如下表，规定75分以下为一般，大于等于75分小于85分为良好，85分及以上为优秀．
分数 | 69 | 73 | 74 | 75 | 77 | 78 | 79 | 80 | 82 | 83 | 85 | 87 | 89 | 93 | 95 | 合计 |
人数 | 2 | 4 | 4 | 2 | 3 | 4 | 6 | 3 | 3 | 4 | 4 | 5 | 2 | 3 | 1 | 50 |
经计算，样本的平均值
，标准差
．为评判该份试卷质量的好坏，从其中任取一人，记其成绩为X，并根据以下不等式进行评判：
①
；
②
；
③
．
评判规则：若同时满足上述三个不等式，则被评为优秀试卷；若仅满足其中两个不等式，则被评为合格试卷；其他情况，则被评为不合格试卷．
（1）试判断该份试卷被评为哪种等级；
（2）按分层抽样的方式从3个层次的学生中抽出10名学生，再从抽出的10名学生中随机抽出4人进行学习方法交流，用随机变量表示4人中成绩优秀的人数，求随机变量
的分布列和数学期望．
