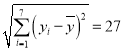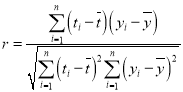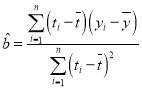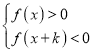题目内容
【题目】在一次考试中,某班级50名学生的成绩统计如下表,规定75分以下为一般,大于等于75分小于85分为良好,85分及以上为优秀.
分数 | 69 | 73 | 74 | 75 | 77 | 78 | 79 | 80 | 82 | 83 | 85 | 87 | 89 | 93 | 95 | 合计 |
人数 | 2 | 4 | 4 | 2 | 3 | 4 | 6 | 3 | 3 | 4 | 4 | 5 | 2 | 3 | 1 | 50 |
经计算,样本的平均值![]() ,标准差
,标准差![]() .为评判该份试卷质量的好坏,从其中任取一人,记其成绩为X,并根据以下不等式进行评判:
.为评判该份试卷质量的好坏,从其中任取一人,记其成绩为X,并根据以下不等式进行评判:
①![]() ;
;
②![]() ;
;
③![]() .
.
评判规则:若同时满足上述三个不等式,则被评为优秀试卷;若仅满足其中两个不等式,则被评为合格试卷;其他情况,则被评为不合格试卷.
(1)试判断该份试卷被评为哪种等级;
(2)按分层抽样的方式从3个层次的学生中抽出10名学生,再从抽出的10名学生中随机抽出4人进行学习方法交流,用随机变量表示4人中成绩优秀的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)该份试卷应被评为合格试卷;
(2)见解析,1.2 .
【解析】
(1)根据频数分布表,计算出![]() ,
,![]()
![]() 的值,由此判断出“该份试卷为合格试卷”;
的值,由此判断出“该份试卷为合格试卷”;
(2)利用超几何分布分布列计算公式,计算出分布列,并求得数学期望.
解:(1)![]() ,
,
![]() ,
,
![]() ,
,
因为考生成绩满足两个不等式,所以该份试卷应被评为合格试卷;
(2)50人中成绩一般、良好及优秀的比例为![]() ,
,
所以所抽出的10人中,成绩优秀的有3人,所以![]() 的取值可能为0,1,2,3,
的取值可能为0,1,2,3,
![]() ,
, ![]() ,
,
![]() ,
,![]() ,
,
所以随机变量![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
故![]() .
.

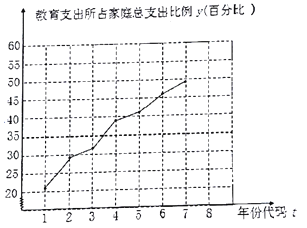
【题目】某工厂生产某种型号的电视机零配件,为了预测今年![]() 月份该型号电视机零配件的市场需求量,以合理安排生产,工厂对本年度
月份该型号电视机零配件的市场需求量,以合理安排生产,工厂对本年度![]() 月份至
月份至![]() 月份该型号电视机零配件的销售量及销售单价进行了调查,销售单价
月份该型号电视机零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的
(单位:千件)之间的![]() 组数据如下表所示:
组数据如下表所示:
月份 |
|
|
|
|
|
|
销售单价 |
|
|
|
|
|
|
销售量 |
|
|
|
|
|
|
(1)根据1至![]() 月份的数据,求
月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(2)结合(1)中的线性回归方程,假设该型号电视机零配件的生产成本为每件![]() 元,那么工厂如何制定
元,那么工厂如何制定![]() 月份的销售单价,才能使该月利润达到最大(计算结果精确到
月份的销售单价,才能使该月利润达到最大(计算结果精确到![]() )?
)?
参考公式:回归直线方程![]() ,其中
,其中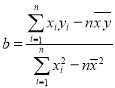 .
.
参考数据:![]() .
.
【题目】每个国家对退休年龄都有不一样的规定,从2018年开始,我国关于延迟退休的话题一直在网上热议,为了了解市民对“延迟退休”的态度,现从某地市民中随机选取100人进行调查,调查情况如下表:
年龄段(单位:岁) |
|
|
|
|
|
|
被调查的人数 |
|
|
|
|
|
|
赞成的人数 |
|
|
|
|
|
|
(1)从赞成“延迟退休”的人中任选1人,此人年龄在![]() 的概率为
的概率为![]() ,求出表格中
,求出表格中![]() 的值;
的值;
(2)若从年龄在![]() 的参与调查的市民中按照是否赞成“延迟退休”进行分层抽样,从中抽取10人参与某项调查,然后再从这10人中随机抽取4人参加座谈会,记这4人中赞成“延迟退休”的人数为
的参与调查的市民中按照是否赞成“延迟退休”进行分层抽样,从中抽取10人参与某项调查,然后再从这10人中随机抽取4人参加座谈会,记这4人中赞成“延迟退休”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.