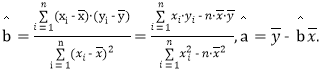题目内容
【题目】在区间[0，2]上任取两个实数a，b，则函数f（x）=x3+ax﹣b在区间[﹣1，1]上有且只有一个零点的概率是（ ）
A.
B.
C.
D.
【答案】D
【解析】解：由题意知本题是一个几何概型， ∵a∈[0，2]，
∴f'（x）=3x2+a≥0，
∴f（x）是增函数
若f（x）在[﹣1，1]有且仅有一个零点，
则f（﹣1）f（1）≤0
∴（﹣1﹣a﹣b）（1+a﹣b）≤0，
即（1+a+b）（1+a﹣b）≥0 
= 
11
由线性规划内容知全部事件的面积为2×2=4，满足条件的面积4﹣ = 
∴P= 
= 
故选D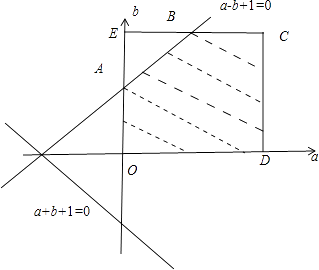
【考点精析】掌握几何概型和函数的零点是解答本题的根本，需要知道几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等；函数的零点就是方程的实数根，亦即函数的图象与轴交点的横坐标．即：方程有实数根，函数的图象与坐标轴有交点，函数有零点．
练习册系列答案
阅读快车系列答案
相关题目
【题目】参与舒城中学数学选修课的同学对某公司的一种产品销量与价格进行了统计,得到如下数据和散点图.
定价x(元/千克) | 10 | 20 | 30 | 40 | 50 | 60 |
年销量y(千克) | 1150 | 643 | 424 | 262 | 165 | 86 |
z=2 ln y | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |
参考数据:
，
.
(1)根据散点图判断y与x,z与x哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
(2)根据(1)的判断结果及数据,建立y关于x的回归方程(方程中的系数均保留两位有效数字).
(3)当定价为150元/千克时,试估计年销量.
附:对于一组数据(x1,y1),(x2,y2),(x3,y3),…,(xn,yn),其回归直线
x+
的斜率和截距的最
小二乘估计分别为
