��Ŀ����
����Ŀ�����������ѧ��ѧѡ�ε�ͬѧ��ij��˾��һ�ֲ�Ʒ������۸������ͳ��,�õ��������ݺ�ɢ��ͼ.
����x(Ԫ/ǧ��) | 10 | 20 | 30 | 40 | 50 | 60 |
������y(ǧ��) | 1150 | 643 | 424 | 262 | 165 | 86 |
z=2 ln y | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |

�����:
![]() ��
��
![]() .
.
(1)����ɢ��ͼ�ж�y��x,z��x��һ�Ծ��н�ǿ�����������(�����жϼ���,����˵������)?
(2)����(1)���жϽ��������,����y����x�Ļع鷽��(�����е�ϵ����������λ��Ч����).
(3)������Ϊ150Ԫ/ǧ��ʱ,�Թ���������.
��:����һ������(x1,y1),(x2,y2),(x3,y3),��,(xn,yn),��ع�ֱ��![]() x+
x+![]() ��б�ʺͽؾ����
��б�ʺͽؾ����
С���˹��Ʒֱ�Ϊ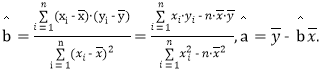
���𰸡�(1) z��x���н�ǿ�����������(2)![]() ��3������������Ϊ
��3������������Ϊ![]() =1ǧ��
=1ǧ��
��������
![]() ��ɢ��ͼ��֪z��x��Ӧ��ɢ��ͼ��������һ��ֱ�߸�������������Ը�ǿ
��ɢ��ͼ��֪z��x��Ӧ��ɢ��ͼ��������һ��ֱ�߸�������������Ը�ǿ
![]() ���ݹ�ʽ������ع鷽�̵�ϵ��������д���ع鷽��
���ݹ�ʽ������ع鷽�̵�ϵ��������д���ع鷽��
![]() ����ع鷽�����������
����ع鷽�����������
(1)��ɢ��ͼ֪, z��x���н�ǿ�����������.
(2)��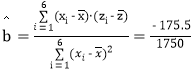 ��-0.10,
��-0.10,
��![]() ��15,��
��15,��![]() x+
x+![]() =15-0.10x.
=15-0.10x.
����z=2ln y,��y����x�Ļع鷽��Ϊ![]() .
.
(3)������Ϊ150Ԫ/ǧ��ʱ,����������Ϊ![]() =1ǧ��.
=1ǧ��.

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ


