题目内容
【题目】已知![]() 为实数,
为实数,![]() .
.
(1)若![]() ,求
,求![]() 在
在![]() 上的最大值和最小值;
上的最大值和最小值;
(2)若![]() 在
在![]() 和
和![]() 上都递减,求
上都递减,求![]() 的取值范围.
的取值范围.
【答案】(1)最大值为22,最小值为![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)首先求出导函数,然后根据导函数与0的关系求出函数![]() 的单调区间,由此求得最大值与最小值;(2)根据函数的单调性与导函数的关系,结合判别式建立不等式组求解即可.
的单调区间,由此求得最大值与最小值;(2)根据函数的单调性与导函数的关系,结合判别式建立不等式组求解即可.
试题解析:f(x)=-3x2+6ax+2a+7.
(1)f(-1)=-4a+4=0,所以a=1. …2分
f(x)=-3x2+6x+9=-3(x-3)(x+1),
当-2≤x<-1时,f(x)<0,f(x)单调递减;
当-1<x≤2时,f(x)>0,f(x)单调递增,
又f(-2)=2,f(-1)=-5,f(2)=22,
故f(x)在[-2,2]上的最大值为22,最小值为-5. …6分
(2)由题意得x∈(-∞,-2]∪[3,+∞)时,f(x)≤0成立, …7分
由f(x)=0可知,判别式>0,所以解得:-≤a≤1.
所以a的取值范围为[-,1]. …12分

练习册系列答案
相关题目
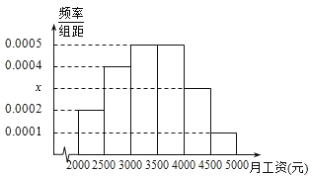
【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表:
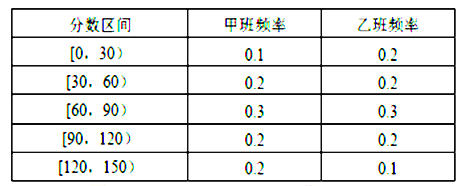
(1)若成绩120分以上(含120分)为优秀,求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(2)根据以上数据完成下面的![]() 列联表:在犯错概率小于
列联表:在犯错概率小于![]() 的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?
的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?

| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
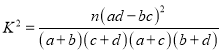 ,其中
,其中![]() .
.