题目内容
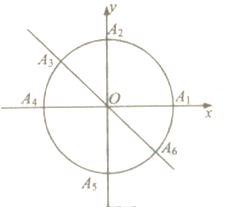
【题目】如图,四棱锥![]() 中,
中,![]() 底面
底面![]() 为线段
为线段![]() 上一点,
上一点,![]() 为
为![]() 的中点.
的中点.
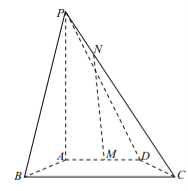
(1)证明:![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连
,连![]() ,然后利用中位线定理结合已知条件证明得
,然后利用中位线定理结合已知条件证明得![]() 是平行四边形,从而利用平行四边形的性质可使问题得证;(2)根据已知条件结合线面垂直的性质定理推出
是平行四边形,从而利用平行四边形的性质可使问题得证;(2)根据已知条件结合线面垂直的性质定理推出![]() 平面
平面![]() ,由此可求得
,由此可求得![]() 点到平面
点到平面![]() 的距离.
的距离.
试题解析:(1)过N作NE∥BC,交PB于点E,连AE,
∵CN=3NP,∴EN∥BC且EN=BC,
又∵AD∥BC,BC=2AD=4,M为AD的中点,
∴AM∥BC且AM=BC,∴EN∥AM且EN=AM,
∴四边形AMNE是平行四边形,∴MN∥AE,
又∵MN平面PAB,AE平面PAB,∴MN∥平面PAB. …6分
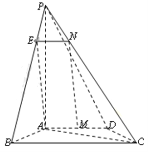
(2)连接AC,在梯形ABCD中,
由BC=2AD=4,AB=CD,∠ABC=60°,得AB=2,∴AC=2,AC⊥AB.
∵PA⊥平面ABCD,∴PA⊥AC.
又∵PA∩AB=A,∴AC⊥平面PAB.
又∵CN=3NP,∴N点到平面PAB的距离d=AC=. …12分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某汽车公司为确定下一年度投入某种产品的宣传费,需了解年宣传费(单位:千元)对年利润![]() (单位:万元)的影响,对近5年的宣传费
(单位:万元)的影响,对近5年的宣传费![]() 和年利润
和年利润![]() (
(![]() )进行了统计,列出了下表:
)进行了统计,列出了下表:
| 2 | 4 | 7 | 17 | 30 |
| 1 | 2 | 3 | 4 | 5 |
员工小王和小李分别提供了不同的方案.
(1)小王准备用线性回归模型拟合![]() 与
与![]() 的关系,请你帮助建立
的关系,请你帮助建立![]() 关于
关于![]() 的线性回归方程;(系数精确到0.01)
的线性回归方程;(系数精确到0.01)
(2)小李决定选择对数回归模型拟合![]() 与
与![]() 的关系,得到了回归方程:
的关系,得到了回归方程: ![]() ,并提供了相关指数
,并提供了相关指数![]() .请用相关指数说明哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析数据
.请用相关指数说明哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析数据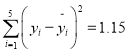 )
)
参考公式:相关指数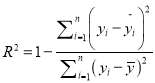
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: 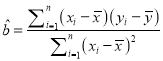 ,
, ![]() .参考数据:
.参考数据: ![]() ,
, ![]() .
.