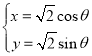题目内容
【题目】已知函数![]() .
.
(1)求![]() 的最大值;
的最大值;
(2)当![]() 时,函数
时,函数![]() 有最小值. 记
有最小值. 记![]() 的最小值为
的最小值为![]() ,求函数
,求函数![]() 的值域.
的值域.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)首先求得导函数,然后根据导函数与0的关系求得函数![]() 的单调区间,从而求得
的单调区间,从而求得![]() 的最大值;(2)首先求得
的最大值;(2)首先求得![]() ,然后结合(1)分
,然后结合(1)分![]() 、
、![]() 求得函数的单调区间与最小值的函数解析式,再通过求导研究其的单调性,从而求得
求得函数的单调区间与最小值的函数解析式,再通过求导研究其的单调性,从而求得![]() 的值域.
的值域.
试题解析:(1)f′(x)=(x>0),
当x∈(0,e)时,f′(x)>0,f(x)单调递增;
当x∈(e,+∞)时,f′(x)<0,f(x)单调递减,
所以当x=e时,f(x)取得最大值f(e)=. …4分
(2)g′(x)=lnx-ax=x(-a),由(1)及x∈(0,e]得:
①当a=时,-a≤0,g′(x)≤0,g(x)单调递减,
当x=e时,g(x)取得最小值g(e)=h(a)=-. …6分
②当a∈[0,),f(1)=0≤a,f(e)=>a,
所以存在t∈[1,e),g′(t)=0且lnt=at,
当x∈(0,t)时,g′(x)<0,g(x)单调递减,当x∈(t,e]时,g′(x)>0,g(x)单调递增,
所以g(x)的最小值为g(t)=h(a). …9分
令h(a)=G(t)=-t,
因为G′(t)=<0,所以G(t)在[1,e)单调递减,此时G(t)∈(-,-1].
综上,h(a)∈[-,-1]. …12分

【题目】葫芦岛市某高中进行一项调查:2012年至2016年本校学生人均年求学花销![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
年求学花销 | 3.2 | 3.5 | 3.8 | 4.6 | 4.9 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2012年至2016年本校学生人均年求学花销的变化情况,并预测该地区2017年本校学生人均年求学花销情况.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
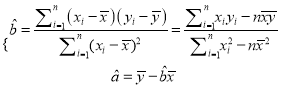
【题目】某汽车公司为确定下一年度投入某种产品的宣传费,需了解年宣传费(单位:千元)对年利润![]() (单位:万元)的影响,对近5年的宣传费
(单位:万元)的影响,对近5年的宣传费![]() 和年利润
和年利润![]() (
(![]() )进行了统计,列出了下表:
)进行了统计,列出了下表:
| 2 | 4 | 7 | 17 | 30 |
| 1 | 2 | 3 | 4 | 5 |
员工小王和小李分别提供了不同的方案.
(1)小王准备用线性回归模型拟合![]() 与
与![]() 的关系,请你帮助建立
的关系,请你帮助建立![]() 关于
关于![]() 的线性回归方程;(系数精确到0.01)
的线性回归方程;(系数精确到0.01)
(2)小李决定选择对数回归模型拟合![]() 与
与![]() 的关系,得到了回归方程:
的关系,得到了回归方程: ![]() ,并提供了相关指数
,并提供了相关指数![]() .请用相关指数说明哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析数据
.请用相关指数说明哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析数据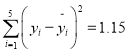 )
)
参考公式:相关指数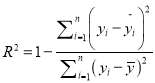
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: 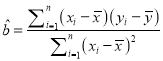 ,
, ![]() .参考数据:
.参考数据: ![]() ,
, ![]() .
.
【题目】近年来我国电子商务行业迎来蓬勃发展的新机遇,2016年双11期间,某平台的销售业绩高达918亿人民币,与此同时,相关管理部门也推出了针对电商的商品和服务评价体系,现从评价系统中随机选出200次成功的交易,并对其评价结果进行统计,对商品的好评率为![]() ,对服务的好评率为
,对服务的好评率为![]() ,其中对商品和服务都做出好评的交易为80次.
,其中对商品和服务都做出好评的交易为80次.
在犯错误概率不超过( )的前提下,认为商品好评与服务好评有关.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()