Question

【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试，分数分布如表：

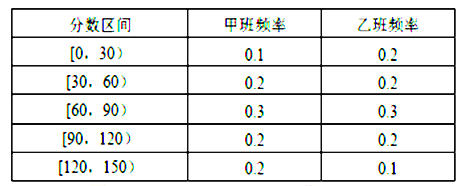
（1）若成绩120分以上（含120分）为优秀，求从乙班参加测试的90分以上（含90分）的同学中，随机任取2名同学，恰有1人为优秀的概率；

（2）根据以上数据完成下面的列联表：在犯错概率小于的前提下，你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系？

	2.072	2.706	3.841	5.024	6.635	7.879	10.828
	0.15	0.10	0.05	0.025	0.010	0.005	0.001

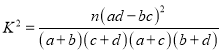，其中.

Answer 1

【答案】（1）（2）在犯错概率小于0.1的前提下，没有足够的把握说明学生的数学成绩是否优秀与班级有关系.

【解析】试题分析：（1）计算乙班参加测试的90(分)以上的同学人数,以及120分以人数,利用列举法求出对应事件数,求出对应的概率值;
（2）计算甲、乙两班优秀与不优秀的人数,填写列联表,计算,对照数表得出概率结论.

试题解析：（1）乙班参加测试的90（分）以上的同学有人，记为，其中成绩优秀120分以上有人，记为，从这6名学生随机抽取两名的基本事件有：

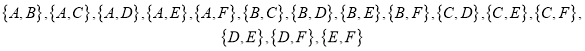
共15个，设事件表示恰有一位学生成绩优秀，符合要求的事件有共8个；

所以；

（2）计算甲班优秀的人数为，不优秀的人数为16，乙班优秀人数为2，不优秀的人数为18，填写列联表，如下：

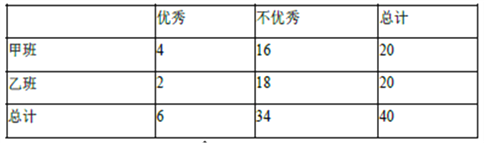
计算；

所以在犯错概率小于0.1的前提下，没有足够的把握说明学生的数学成绩是否优秀与班级有关系.