题目内容
已知等比数列{an}满足:|a2-a3|=10,a1a2a3=125.
(1)求数列{an}的通项公式;
(2)是否存在正整数m,使得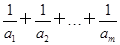 ≥1?若存在,求m的最小值;若不存在,说明理由.
≥1?若存在,求m的最小值;若不存在,说明理由.
(1)求数列{an}的通项公式;
(2)是否存在正整数m,使得
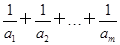 ≥1?若存在,求m的最小值;若不存在,说明理由.
≥1?若存在,求m的最小值;若不存在,说明理由.(1)an=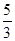 ·3n-1或an=-5·(-1)n-1.(2)不存在
·3n-1或an=-5·(-1)n-1.(2)不存在
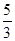 ·3n-1或an=-5·(-1)n-1.(2)不存在
·3n-1或an=-5·(-1)n-1.(2)不存在(1)设等比数列{an}的公比为q,则由已知可得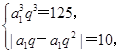
解得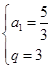 或
或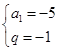
故an=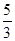 ·3n-1或an=-5·(-1)n-1.
·3n-1或an=-5·(-1)n-1.
(2)若an=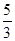 ·3n-1,则
·3n-1,则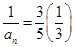 n-1,
n-1,
则数列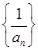 是首项为
是首项为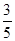 ,公比为
,公比为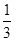 的等比数列.
的等比数列.
从而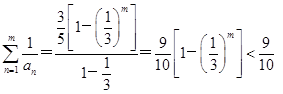 <1.
<1.
若an=-5·(-1)n-1,则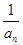 =-
=- (-1)n-1,
(-1)n-1,
故数列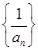 是首项为-
是首项为- ,公比为-1的等比数列,
,公比为-1的等比数列,
从而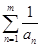 =
=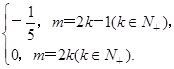 故
故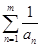 <1.
<1.
综上,对任何正整数m,总有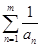 <1.
<1.
故不存在正整数m,使得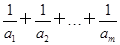 ≥1成立
≥1成立
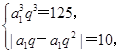
解得
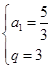 或
或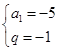
故an=
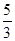 ·3n-1或an=-5·(-1)n-1.
·3n-1或an=-5·(-1)n-1.(2)若an=
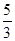 ·3n-1,则
·3n-1,则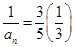 n-1,
n-1,则数列
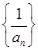 是首项为
是首项为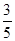 ,公比为
,公比为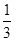 的等比数列.
的等比数列.从而
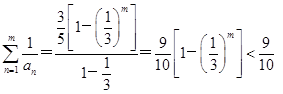 <1.
<1.若an=-5·(-1)n-1,则
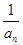 =-
=- (-1)n-1,
(-1)n-1,故数列
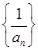 是首项为-
是首项为- ,公比为-1的等比数列,
,公比为-1的等比数列, 从而
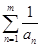 =
=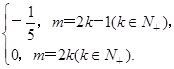 故
故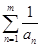 <1.
<1.综上,对任何正整数m,总有
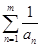 <1.
<1.故不存在正整数m,使得
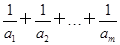 ≥1成立
≥1成立
练习册系列答案
相关题目
 ,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.
,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.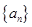 前
前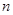 项和为
项和为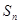 ,且满足
,且满足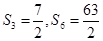 ,
,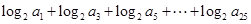 的值.
的值. ,9S3=S6,设Tn=a1a2a3…an,则使Tn取最小值的n值为________.
,9S3=S6,设Tn=a1a2a3…an,则使Tn取最小值的n值为________.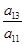 =________.
=________. B.-
B.-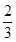 的等比数列{an}的前n项和为Sn,则 ( ).
的等比数列{an}的前n项和为Sn,则 ( ).