题目内容
已知等比数列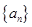 前
前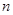 项和为
项和为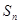 ,且满足
,且满足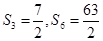 ,
,
(Ⅰ)求数列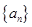 的通项公式;
的通项公式;
(Ⅱ)求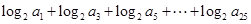 的值.
的值.
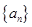 前
前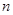 项和为
项和为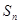 ,且满足
,且满足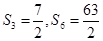 ,
,(Ⅰ)求数列
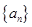 的通项公式;
的通项公式;(Ⅱ)求
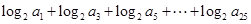 的值.
的值.(1)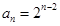 ;(2)143.
;(2)143.
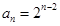 ;(2)143.
;(2)143.试题分析:本题主要考查等差数列与等比数列的概念、通项公式、前n项和公式、数列求和及对数式的运算等数学知识,考查思维能力、分析问题解决问题的能力以及计算能力.第一问,法一:利用等比数列的前n项和公式,将
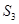 和
和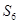 展开,组成方程组,两式相除,解出
展开,组成方程组,两式相除,解出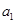 和
和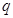 ,写出通项公式;法二:利用等比数列的通项公式,又因为
,写出通项公式;法二:利用等比数列的通项公式,又因为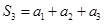 ,
,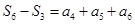 ,展开,相除,解出
,展开,相除,解出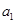 和
和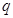 ,写出通项公式;第二问,先将第一问的结论代入,化简
,写出通项公式;第二问,先将第一问的结论代入,化简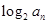 ,得到
,得到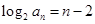 ,所以可以证出数列
,所以可以证出数列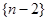 为等差数列,所以利用等差数列的前n项和公式进行求和化简.
为等差数列,所以利用等差数列的前n项和公式进行求和化简.试题解析:(1)法一:
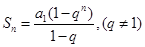
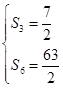 ,整理得
,整理得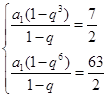 ,解得
,解得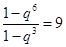 ,
,得
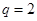 ,
,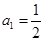 ,所以,通项公式为
,所以,通项公式为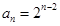 5分
5分法二:
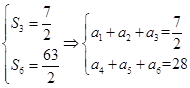 ,得
,得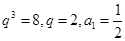 ,所以,通项公式为
,所以,通项公式为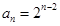 . 5分
. 5分(2)
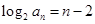 6分
6分则
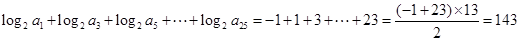 12分
12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
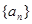 的首项为
的首项为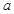 (
(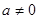 ),前
),前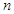 项和为
项和为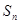 ,且
,且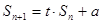 (
(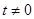 ).设
).设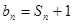 ,
,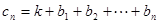 (
(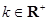 ).
).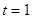 时,若对任意
时,若对任意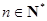 ,
,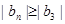 恒成立,求
恒成立,求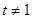 时,试求三个正数
时,试求三个正数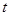 ,
,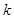 的一组值,使得
的一组值,使得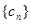 为等比数列,且
为等比数列,且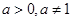 ,数列
,数列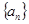 是首项为
是首项为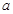 ,公比也为
,公比也为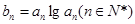
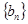 的前
的前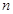 项和
项和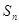 ;
;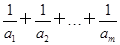 ≥1?若存在,求m的最小值;若不存在,说明理由.
≥1?若存在,求m的最小值;若不存在,说明理由.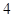 年计算机的价格降低
年计算机的价格降低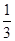 ,则
,则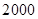 年价格为
年价格为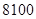 元的计算机到
元的计算机到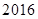 年价格应为( )
年价格应为( ) 元
元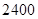 元
元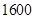 元
元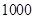 元
元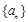 的前
的前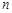 项和为
项和为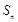 ,若
,若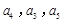 成等差数列,且
成等差数列,且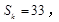
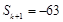 ,其中
,其中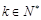 ,则
,则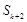 的值为 .
的值为 .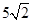
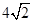
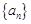 为等比数列,
为等比数列,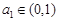 ,
,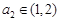 ,
,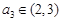 ,则
,则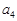 的取值范围是( )
的取值范围是( )

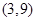

 中,
中,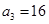 ,
,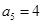 ,则
,则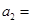 .
.