题目内容
在平面直角坐标系中,已知焦距为4的椭圆 的左、右顶点分别为
的左、右顶点分别为 ,椭圆
,椭圆 的右焦点为
的右焦点为 ,过
,过 作一条垂直于
作一条垂直于 轴的直线与椭圆相交于
轴的直线与椭圆相交于 ,若线段
,若线段 的长为
的长为 。
。
(1)求椭圆 的方程;
的方程;
(2)设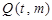 是直线
是直线 上的点,直线
上的点,直线 与椭圆
与椭圆 分别交于点
分别交于点 ,求证:直线
,求证:直线 必过
必过 轴上的一定点,并求出此定点的坐标;
轴上的一定点,并求出此定点的坐标;
 的左、右顶点分别为
的左、右顶点分别为 ,椭圆
,椭圆 的右焦点为
的右焦点为 ,过
,过 作一条垂直于
作一条垂直于 轴的直线与椭圆相交于
轴的直线与椭圆相交于 ,若线段
,若线段 的长为
的长为 。
。(1)求椭圆
 的方程;
的方程;(2)设
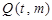 是直线
是直线 上的点,直线
上的点,直线 与椭圆
与椭圆 分别交于点
分别交于点 ,求证:直线
,求证:直线 必过
必过 轴上的一定点,并求出此定点的坐标;
轴上的一定点,并求出此定点的坐标;(1)依题意,椭圆过点 ,故
,故 ,解得
,解得 。…………(2分)
。…………(2分)
椭圆 的方程为
的方程为 。……………………………(5分)
。……………………………(5分)
(2)设 ,直线
,直线 的方程为
的方程为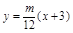 ,……………(6分)
,……………(6分)

代入椭圆方程,得 , ……(7分)
, ……(7分)
设 ,则
,则 ,
,
 ,故点
,故点 的坐标为
的坐标为 。…(8分)
。…(8分)
同理,直线 的方程为
的方程为 ,代入椭圆方程,
,代入椭圆方程,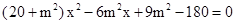 ,
,
设 ,则
,则 ,
, 。
。
可得点 的坐标为
的坐标为 。………………………(10分)
。………………………(10分)
①若 时,直线
时,直线 的方程为
的方程为 ,与
,与 轴交于
轴交于 点;……11
点;……11
②若 ,直线
,直线 的方程为
的方程为 ,…(13分)
,…(13分)
令 ,解得
,解得 。综上所述,直线
。综上所述,直线 必过
必过 轴上的定点
轴上的定点 。
。
 ,故
,故 ,解得
,解得 。…………(2分)
。…………(2分)椭圆
 的方程为
的方程为 。……………………………(5分)
。……………………………(5分)(2)设
 ,直线
,直线 的方程为
的方程为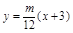 ,……………(6分)
,……………(6分)
代入椭圆方程,得
 , ……(7分)
, ……(7分)设
 ,则
,则 ,
,  ,故点
,故点 的坐标为
的坐标为 。…(8分)
。…(8分)同理,直线
 的方程为
的方程为 ,代入椭圆方程,
,代入椭圆方程,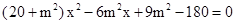 ,
,设
 ,则
,则 ,
, 。
。可得点
 的坐标为
的坐标为 。………………………(10分)
。………………………(10分)①若
 时,直线
时,直线 的方程为
的方程为 ,与
,与 轴交于
轴交于 点;……11
点;……11②若
 ,直线
,直线 的方程为
的方程为 ,…(13分)
,…(13分)令
 ,解得
,解得 。综上所述,直线
。综上所述,直线 必过
必过 轴上的定点
轴上的定点 。
。略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的右焦点为
的右焦点为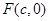 且
且 ,设短轴的一个端点为
,设短轴的一个端点为 ,原点
,原点 到直线
到直线 的距离为
的距离为 ,过原点和
,过原点和 轴不重合的直线与椭圆
轴不重合的直线与椭圆 相交于
相交于 两点,且
两点,且 .
. 的直线
的直线 与椭圆
与椭圆 且使得
且使得 成立?若存在,试求出直线
成立?若存在,试求出直线 +
+ =1
=1 的左.右焦点为
的左.右焦点为 ,离心率为
,离心率为 ,直线
,直线 与x轴、y轴分别交于点
与x轴、y轴分别交于点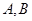 ,
, 是直线
是直线 与椭圆C的一个公共点,
与椭圆C的一个公共点, 是点
是点 关于直线
关于直线 =
=
 ; (Ⅱ)确定
; (Ⅱ)确定 的值,使得
的值,使得 是等腰三角形.
是等腰三角形. 的坐标分别为
的坐标分别为 ,
, ,并且经过点
,并且经过点 .过左焦点
.过左焦点 ,斜率为
,斜率为 的直线与椭圆交于
的直线与椭圆交于 ,
, 两点.设
两点.设 ,延长
,延长 ,
, 分别与椭圆交于
分别与椭圆交于 两点.
两点. ,求
,求 点的坐标;
点的坐标; 的斜率为
的斜率为 ,求证:
,求证: 为定值.
为定值. 的长轴
的长轴 分成
分成 等份,过每个分点作
等份,过每个分点作 轴的垂线交椭圆的上半部分于
轴的垂线交椭圆的上半部分于 七个点,
七个点, 是椭圆的一个焦点,则
是椭圆的一个焦点,则 ( ).
( ).
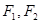 分别是椭圆:
分别是椭圆: 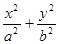 (
(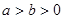 )的左、右焦点,过
)的左、右焦点,过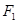 斜率为1的直线
斜率为1的直线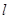 与该椭圆相交于P,Q两点,且
与该椭圆相交于P,Q两点,且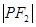 ,
, ,
,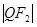 成等差数列.
成等差数列. 中,
中,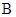 为椭圆上的一点,过坐标原点
为椭圆上的一点,过坐标原点 的直线交椭圆于
的直线交椭圆于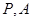 两点,其中
两点,其中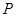 在第一象限,过
在第一象限,过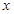 轴的垂线,垂足为
轴的垂线,垂足为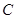 ,连接
,连接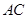 ,
, 与
与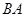 的斜率均存在,问它们的斜率之积是否为定值,若是,求出这个定值,若不是,说明理由;
的斜率均存在,问它们的斜率之积是否为定值,若是,求出这个定值,若不是,说明理由;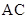 的延长线与椭圆的交点,求证:
的延长线与椭圆的交点,求证: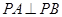 .
. 的一个焦点坐标为(0,1),则实数
的一个焦点坐标为(0,1),则实数 的值等于_____ ____,
的值等于_____ ____, 的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率
的准线与x轴交于F1,焦点为F2;以F1,F2为焦点,离心率 的椭圆C2与抛物线C1在X轴上方的交点为P,延长PF2交抛物线于点Q,M是抛物线上一动点,且M在P与Q之间运动.
的椭圆C2与抛物线C1在X轴上方的交点为P,延长PF2交抛物线于点Q,M是抛物线上一动点,且M在P与Q之间运动. 的边长恰好是三个连续的自然数时,求
的边长恰好是三个连续的自然数时,求 面积的最大值.
面积的最大值.