题目内容
13.已知$\frac{1+tan(π+α)}{1+tan(2π-α)}$=-3,求cos2(π-α)+sin($\frac{3π}{2}$+α)•cos($\frac{π}{2}$+α)+2sin2(α-π)的值.分析 由$\frac{1+tan(π+α)}{1+tan(2π-α)}$=-3运用诱导公式化简求值可得tanα=2,由诱导公式,倍角公式,万能公式化简所求即可得解.
解答 解:∵$\frac{1+tan(π+α)}{1+tan(2π-α)}$=-3⇒$\frac{1+tanα}{1-tanα}$=-3⇒1+tanα=-3+3tanα⇒tanα=2,
∴cos2(π-α)+sin($\frac{3π}{2}$+α)•cos($\frac{π}{2}$+α)+2sin2(α-π)
=cos2α+cosα•sinα+2sin2α
=1+$\frac{1-cos2α}{2}$+$\frac{1}{2}$sin2α
=$\frac{3}{2}$+$\frac{1}{2}$(sin2α-cos2α)
=$\frac{3}{2}$+$\frac{1}{2}×\frac{2tanα}{1+ta{n}^{2}α}$-$\frac{1}{2}×\frac{1-ta{n}^{2}α}{1+ta{n}^{2}α}$
=$\frac{3}{2}$+$\frac{1}{2}×\frac{4}{5}$-$\frac{1}{2}×\frac{-3}{5}$
=$\frac{11}{5}$.
点评 本题主要考查了运用诱导公式化简求值,同角三角函数基本关系的运用,熟练使用相关公式是解题的关键,属于基本知识的考查.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
3.b,c表示两条不重合的直线,α,β表示两个不重合的平面,下列命题中正确的是( )
| A. | $\left.\begin{array}{l}{c∥α}\\{b?α}\end{array}\right\}$⇒c∥b | B. | $\left.\begin{array}{l}{c∥α}\\{α⊥β}\end{array}\right\}$⇒c⊥β | C. | $\left.\begin{array}{l}{c⊥α}\\{c⊥β}\end{array}\right\}$⇒α∥β | D. | $\left.\begin{array}{l}{b∥c}\\{c?α}\end{array}\right\}$⇒b∥α |
4.已知函数f(x)满足f(x+4)=f(x),且当-1<x≤3时,f(x)=$\left\{\begin{array}{l}{m\sqrt{1-{x}^{2}},x∈(-1,1]}\\{1-|x-2|,x∈(1,3]}\end{array}\right.$.其中m>0,若方程3f(x)-x=0恰好有5个根,则实数m的取值范围是( )
| A. | ($\frac{\sqrt{15}}{3}$,$\sqrt{7}$) | B. | ($\frac{\sqrt{15}}{3}$,$\frac{8}{3}$) | C. | ($\frac{4}{3}$,$\sqrt{7}$) | D. | ( $\frac{4}{3}$,$\frac{8}{3}$) |
1.设复数z1=-1+i,z2=$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i,则$\frac{{z}_{1}}{{z}_{2}}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.设集合A={x|x2-6x+8<0},B={x|2<2x<8},则A∩B=( )
| A. | {x|1<x<4} | B. | {x|1<x<3} | C. | {x|2<x<3} | D. | {x|3<x<4} |
2.某几何体的三视图如图所示,它的表面积为( )
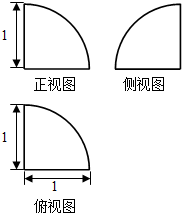

| A. | $\frac{π}{4}$ | B. | $\frac{5π}{4}$ | C. | $\frac{7π}{8}$ | D. | π |
3.已知点A的坐标为(4$\sqrt{3}$,1),将OA绕坐标原点O逆时针旋转$\frac{π}{3}$至OB,则点B的纵坐标为( )
| A. | $\frac{{3\sqrt{3}}}{2}$ | B. | $\frac{{5\sqrt{3}}}{2}$ | C. | $\frac{11}{2}$ | D. | $\frac{13}{2}$ |
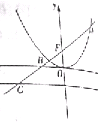 如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=$\sqrt{2}$|BF|,且|AF|=4+2$\sqrt{2}$,则p=2.
如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=$\sqrt{2}$|BF|,且|AF|=4+2$\sqrt{2}$,则p=2.