题目内容
5.已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的右焦点F2是抛物线y2=4x的焦点,过点F2垂直于x轴的直线被椭圆C所截得的线段长度为3.(Ⅰ)求椭圆C的方程;
(Ⅱ)设动直线l:y=kx+m与椭圆C有且只有一个公共点 P,且与直线x=2相交于点Q.请问:在x轴上是否存在定点 M,使得$\overrightarrow{{M}{P}}•\overrightarrow{{M}Q}$为定值?若存在,求出点 M的坐标;若不存在,请说明理由.
分析 (Ⅰ)求得抛物线的焦点,由题意可得,椭圆C过点(1,±$\frac{3}{2}$),代入椭圆方程,解方程可得a,b,进而得到椭圆方程;
(Ⅱ)假设在x轴上存在定点M(x1,0)满足条件,设P(x0,y0),则Q(2,2k+m),联立直线l方程和椭圆方程,运用判别式为0,求得m,k的关系,再由向量的数量积的坐标表示,化简整理,即可得到定值.
解答 解:(Ⅰ)抛物线y2=4x的焦点坐标为(1,0),
则由题意可得,椭圆C过点(1,±$\frac{3}{2}$),
则$\left\{\begin{array}{l}{{a}^{2}={b}^{2}+1}\\{\frac{1}{{a}^{2}}+\frac{9}{4{b}^{2}}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}^{2}=4}\\{{b}^{2}=3}\end{array}\right.$,
∴椭圆C的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(Ⅱ)假设在x轴上存在定点M(x1,0)满足条件,设P(x0,y0),
则Q(2,2k+m),
由$\left\{\begin{array}{l}{y=kx+m}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$,得(3+4k2)x2+8kmx+4m2-12=0,
∴△=64k2m2-4(3+4k2)(4m2-12)=0,
即3+4k2=m2,m≠0.
此时x0=-$\frac{4km}{3+4{k}^{2}}$=-$\frac{4k}{m}$,y0=kx0+m=$\frac{3}{m}$,则P(-$\frac{4k}{m}$,$\frac{3}{m}$),
∴$\overrightarrow{MP}$=(-$\frac{4k}{m}$-x1,$\frac{3}{m}$),$\overrightarrow{MQ}$=(2-x1,2k+m),
∴$\overrightarrow{MP}•\overrightarrow{MQ}$=(-$\frac{4k}{m}$-x1)(2-x1)+$\frac{3}{m}$(2k+m)=(4x1-2)•$\frac{k}{m}$+x12-2x1+3,
∴当4x1-2=0即x1=$\frac{1}{2}$时,x12-2x1+3=$\frac{9}{4}$.
∴存在点M($\frac{1}{2}$,0),使得$\overrightarrow{{M}{P}}•\overrightarrow{{M}Q}$为定值$\frac{9}{4}$.
点评 本题考查椭圆的方程和性质,主要考查椭圆的焦点和点满足椭圆方程,同时考查直线方程和椭圆方程联立,运用判别式为0和向量数量积的坐标表示,考查运算能力,属于中档题.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,且AC=BC=CC1=2,M是AB1与A1B的交点,N是B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,且AC=BC=CC1=2,M是AB1与A1B的交点,N是B1C1的中点.(Ⅰ)求证:MN∥平面ACC1A1;
(Ⅱ)求三棱锥N-A1BC的体积.
| A. | 0.94 | B. | 0.97 | C. | 0.06 | D. | 0.03 |
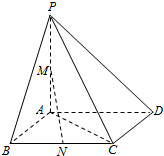 如图,四棱锥P-ABCD中,PA=AB=1,PA⊥底面ABCD,底面ABCD为正方形,且M,N分别为PA与BC的中点
如图,四棱锥P-ABCD中,PA=AB=1,PA⊥底面ABCD,底面ABCD为正方形,且M,N分别为PA与BC的中点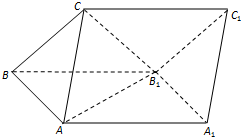 如图,三棱柱ABC-A1B1C1的侧面ABB1A1为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.
如图,三棱柱ABC-A1B1C1的侧面ABB1A1为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.