题目内容
13.已知函数f(x)=cos(2x+$\frac{π}{3}$)+sin2x.(1)求函数f(x)的最小周期;
(2)求函数f(x)的最大值,并求此时x的集合.
分析 先将函数f(x)=cos(2x+$\frac{π}{3}$)+sin2x.化成“一角一函”形式,再求得最小正周期和最值.
解答 解:f(x)=$\frac{1}{2}cos2x-\frac{\sqrt{3}}{2}sin2x+\frac{1-cos2x}{2}$
=$\frac{1}{2}-\frac{\sqrt{3}}{2}sin2x$
(1)所以函数f(x)的最小周期T=$\frac{2π}{2}=π$
(2)当sin2x=-1时,f(x)取得最大值,此时x=2kπ$-\frac{π}{2}$,k∈Z
所以f(x)的最大值为$\frac{1+\sqrt{3}}{2}$,x的取值集合为{x|x=2kπ$-\frac{π}{2}$,k∈Z}.
点评 本题主要考查三角函数的化简,考查了和差公式和降幂公式的应用,属于基础题型.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
1.已知数列{an}满足$\frac{{a}_{n+1}+{a}_{n}-1}{{a}_{n+1}-{a}_{n}+1}$=n(n∈N*),且a4=28,则首项a1=1,通项公式an=(2n-1)n.
18.在等比数列{an}中,a1=5,q=1,则S6=( )
| A. | 5 | B. | 0 | C. | 不存在 | D. | 30 |
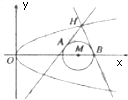 如图,已知⊙M:(x-4)2+y2=1和抛物线C:y2=2px(p>0,其焦点为F),且$\overrightarrow{FM}$=($\frac{15}{4}$,0,),过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切于A、B两点.
如图,已知⊙M:(x-4)2+y2=1和抛物线C:y2=2px(p>0,其焦点为F),且$\overrightarrow{FM}$=($\frac{15}{4}$,0,),过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切于A、B两点.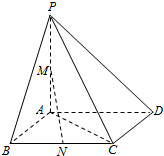 如图,四棱锥P-ABCD中,PA=AB=1,PA⊥底面ABCD,底面ABCD为正方形,且M,N分别为PA与BC的中点
如图,四棱锥P-ABCD中,PA=AB=1,PA⊥底面ABCD,底面ABCD为正方形,且M,N分别为PA与BC的中点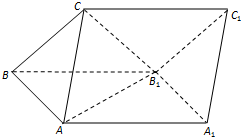 如图,三棱柱ABC-A1B1C1的侧面ABB1A1为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.
如图,三棱柱ABC-A1B1C1的侧面ABB1A1为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.