题目内容
3.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,四个顶点所围成的菱形的面积为8$\sqrt{2}$.(1)求椭圆的方程;
(2)已知直线y=kx+m与椭圆C交于两个不同的点A(x1,y1)和点B(x2,y2),O为坐标原点,且kOA•kOB=-$\frac{1}{2}$,求y1y2的取值范围.
分析 (1)利用菱形的面积和椭圆的性质即可得出;
(2)联立直线方程和椭圆方程,消去y,运用韦达定理和判别式大于0,以及直线的斜率公式,化简整理,即可得到y1y2的范围.
解答 解:(1)由已知可得e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,$\frac{1}{2}$•2a•2b=8$\sqrt{2}$,
又a2=b2+c2,
解得c=2,b=2,a2=8.
∴椭圆的方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1.
(2)直线L:y=kx+m与椭圆C交于两个不同点A(x1,x2)和B(x2,y2),
联立$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+2{y}^{2}=8}\end{array}\right.$,得(1+2k2)x2+4kmx+2m2-8=0,
△=16k2m2-4(1+2k2)(2m2-8)>0,化为8k2+4>m2,①
∴x1+x2=$\frac{-4km}{1+2{k}^{2}}$,x1x2=$\frac{2{m}^{2}-8}{1+2{k}^{2}}$.
∵满足kOA•kOB=-$\frac{1}{2}$,
∴$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{2}$.
∴y1y2=-$\frac{1}{2}$x1x2=-$\frac{1}{2}$•$\frac{2{m}^{2}-8}{1+2{k}^{2}}$=-$\frac{{m}^{2}-4}{1+2{k}^{2}}$,
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2
=k2•$\frac{2{m}^{2}-8}{1+2{k}^{2}}$+km•$\frac{-4km}{1+2{k}^{2}}$+m2=$\frac{{m}^{2}-8{k}^{2}}{1+2{k}^{2}}$.
∴-$\frac{{m}^{2}-4}{1+2{k}^{2}}$=$\frac{{m}^{2}-8{k}^{2}}{1+2{k}^{2}}$.
∴4k2+2=m2,
即有y1y2=-$\frac{{m}^{2}-4}{1+2{k}^{2}}$=-$\frac{2+4{k}^{2}-4}{1+2{k}^{2}}$=$\frac{4}{1+2{k}^{2}}$-2,
则y1y2∈(-2,2].
点评 本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、直线的斜率公式、菱形的面积计算公式等基础知识与基本技能方法,考查了推理能力和计算能力,属于中档题.

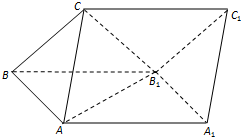 如图,三棱柱ABC-A1B1C1的侧面ABB1A1为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.
如图,三棱柱ABC-A1B1C1的侧面ABB1A1为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C. 如图,直线l:y=-x+1与椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A、B两点.
如图,直线l:y=-x+1与椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A、B两点.