题目内容
19．
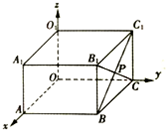如图，长方体ABCO-A1B1C1O1中，|OA|=4，|OC|=6，|OO1|=2，BC1与B1C相交于点P，则点P的坐标是（ ）| A． | （6，2，1） | B． | （1，2，6） | C． | （4，6，2） | D． | （2，6，1） |
分析 根据图中直角坐标系，得出点B、C1的坐标，再求出BC1的中点坐标P．
解答 解：根据题意，得；
点B（4，6，0），点C1（0，6，2），
且P是BC1的中点，
∴P（$\frac{4+0}{2}$，$\frac{6+6}{2}$，$\frac{0+2}{2}$），
即P（2，6，1）．
故选：D．
点评 本题考查了空间直角坐标系的应用问题，是基础题目．
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
9．电灯泡使用时间在1000小时以上概率为0.2，则3个灯泡在使用1000小时后坏了1个的概率是（ ）
| A． | 0.128 | B． | 0.096 | C． | 0.104 | D． | 0.384 |
已知函数f（x）=$\sqrt{3}sin2x-2{sin^2}$x+2，x∈R
7．现有如下投资方案，一年后投资盈亏的情况如下：
（1）投资股市：
（2）购买基金：
（Ⅰ）已知甲、乙两人分别选择了“投资股市”和“购买基金”进行投资，如果一年后他们中至少有一人获利的概率大于$\frac{4}{5}$，求p的取值范围；
（Ⅱ）丙要将家中闲置的20万元钱进行投资，决定在“投资股市”、“购买基金”，或“等额同时投资股市和购买基金”这三种方案中选择一种，已知$p=\frac{1}{2}$，那么丙选择哪种投资方案，才能使得一年后投资收益的数学期望较大？（其中第三方案须考察两项获利之和的随机变量Z），给出结果并说明理由．
（1）投资股市：
| 投资结果 | 获利40% | 不赔不赚 | 亏损20% |
| 概 率 | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ |
| 投资结果 | 获利20% | 不赔不赚 | 亏损10% |
| 概 率 | p | $\frac{1}{3}$ | q |
（Ⅱ）丙要将家中闲置的20万元钱进行投资，决定在“投资股市”、“购买基金”，或“等额同时投资股市和购买基金”这三种方案中选择一种，已知$p=\frac{1}{2}$，那么丙选择哪种投资方案，才能使得一年后投资收益的数学期望较大？（其中第三方案须考察两项获利之和的随机变量Z），给出结果并说明理由．
