题目内容
4.已知实数a>0,关于x、y的不等式组$\left\{\begin{array}{l}{x-2y+1≥0}\\{x≤a}\\{y+a≥0}\end{array}\right.$表示的平面区域为D,若在平面区域D内存在点P(x0,y0),满足3x0-4y0=5,则a的最小值为$\frac{5}{7}$.分析 作出不等式组对应的平面区域,要使平面区域内存在点点P(x0,y0)满足3x0-4y0=5,则平面区域内必存在一个点在直线3x-4y=5的下方,由图象可得a的取值范围,即可求出a的最小值.
解答  解:作出不等式组对应的平面如图:交点C的坐标为(m,-m),
解:作出不等式组对应的平面如图:交点C的坐标为(m,-m),
直线3x-4y=5的斜率为$\frac{3}{4}$,斜截式方程为$y=\frac{3}{4}x-\frac{5}{4}$,
要使平面区域内存在点P(x0,y0)满足3x0-4y0=5,
则点C(a,-a)必在直线3x0-4y0=5的下方,
即-a$≤\frac{3}{4}a-\frac{5}{4}$,解得a$≥\frac{5}{7}$.
故m的最小值为$\frac{5}{7}$.
故答案为:$\frac{5}{7}$.
点评 本题主要考查线性规划的基本应用,利用数形结合是解决本题的关键,综合性较强.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
19.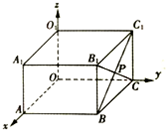 如图,长方体ABCO-A1B1C1O1中,|OA|=4,|OC|=6,|OO1|=2,BC1与B1C相交于点P,则点P的坐标是( )
如图,长方体ABCO-A1B1C1O1中,|OA|=4,|OC|=6,|OO1|=2,BC1与B1C相交于点P,则点P的坐标是( )
 如图,长方体ABCO-A1B1C1O1中,|OA|=4,|OC|=6,|OO1|=2,BC1与B1C相交于点P,则点P的坐标是( )
如图,长方体ABCO-A1B1C1O1中,|OA|=4,|OC|=6,|OO1|=2,BC1与B1C相交于点P,则点P的坐标是( )| A. | (6,2,1) | B. | (1,2,6) | C. | (4,6,2) | D. | (2,6,1) |
9.设扇形的半径长为2cm,面积为4cm2,则扇形的圆心角的弧度数是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
16.在等比数列3,6,12,…中,第5项为( )
| A. | 18 | B. | 24 | C. | 36 | D. | 48 |
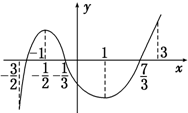 已知函数y=f(x)在定义域$({-\frac{3}{2},3})$上可导,其图象如图,记y=f(x)的导函数y=f′(x),则不等式xf′(x)≤0的解集是[0,1]∪(-$\frac{3}{2}$,-$\frac{1}{2}$].
已知函数y=f(x)在定义域$({-\frac{3}{2},3})$上可导,其图象如图,记y=f(x)的导函数y=f′(x),则不等式xf′(x)≤0的解集是[0,1]∪(-$\frac{3}{2}$,-$\frac{1}{2}$].